2.7. 数学的最適化: 関数の最小値を求める

著者: Gaël Varoquaux

Mathematical optimization は関数の最小値 (あるいは最大値や零点) を数値的に探索する問題を扱います。この分野では関数は コスト関数 や 目的関数 あるいは エネルギー と呼ばれます。

ここではブラックボックス化された最適化手法としての scipy.optimize に焦点をあてます: 最適化する関数の数学的表現をあてにしません。表現を利用することで、より効率的にブラックボックス化しない最適化ができることは注意しておいて下さい。

事前準備

• Numpy, Scipy
• matplotlib

参考

参考文献

数学的最適化はとても...数学的です。パフォーマンスが欲しい場合は、本を読むことは労力に見合います:

• Boyd と Vandenberghe による Convex Optimization (pdf がオンラインで無料で利用できます)。

• Nocedal と Wright による Numerical Optimization 。 最急降下法に詳しい。

• Fletcher による Practical Methods of Optimization : いきいきとした説明。

2.7.1. 問題を知る

最適化問題はそれぞれ異なります。問題を知ることで正しいツールを選択することができます。

問題の次元

最適化問題のスケールの多くは 問題の次元 により設定されます、つまり、探索を実行するスカラー変数の数によります。

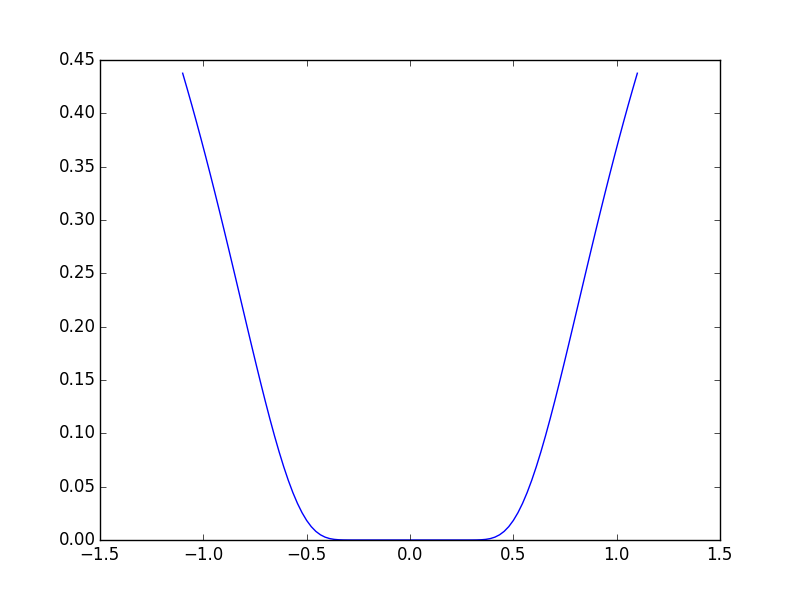
2.7.1.1. 凸関数と非凸関数の最適化の対比

凸関数: f はすべて接線の上に位置します。 つまり、2点 A, B に対して A < C < B ならば f(C) は [f(A), f(B])] の範囲内にあります	非凸関数

凸関数の最適化は簡単です。非凸関数の最適化はとても大変になるかもしれません。

注釈

凸関数の局所最小値は大域的な最小値になることが証明されています。つまり、最小値は一意です。

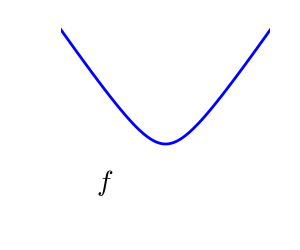
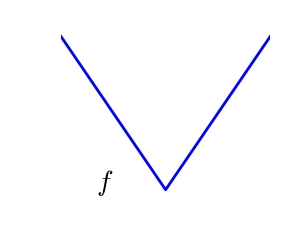
2.7.1.2. 滑らかな場合と滑らかでない場合の問題

滑らかな関数: 勾配がいたるところに定義され、連続な関数	滑らかでない関数

滑かな関数の最適化の方が簡単です (ブラックボックス な条件では真ですが Linear Programming に線形関数の貼り合わせた関数でとても効率的に扱っている方法の例があります)。

2.7.1.3. ノイズがある場合と厳密なコスト関数の対比

ノイズあり(青)とノイズなし(緑) の関数

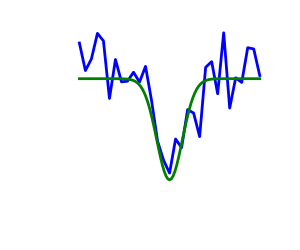勾配のノイズ

多くの最適化手法が目的関数の勾配を利用します。勾配関数が与えられない場合は、数値的に計算されますが、これによってエラーが増えます。そのような状況では、目的関数がノイズを含まない場合であっても、勾配に基づく最適化はノイズを含む最適化になる可能性があります。

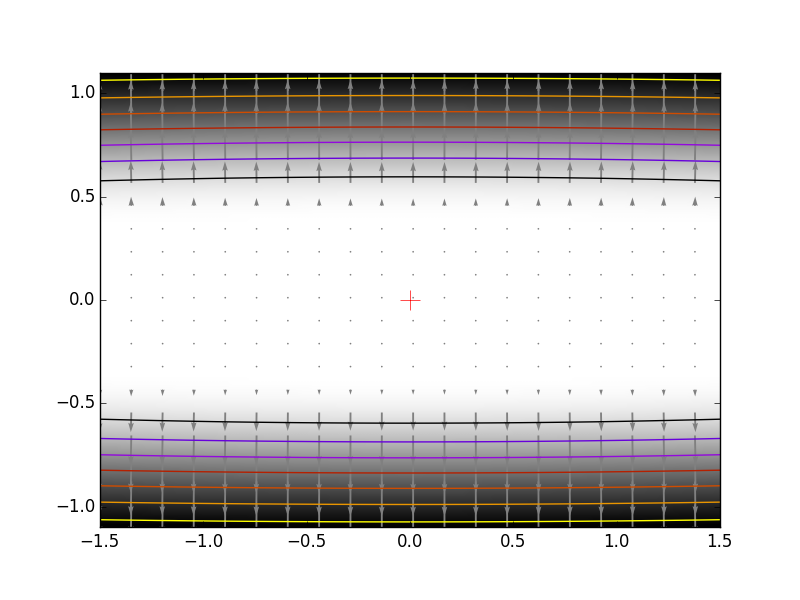
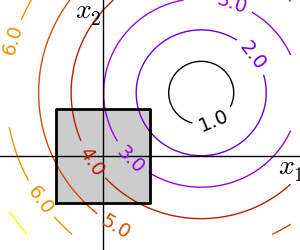
2.7.1.4. 拘束条件

拘束条件のもとでの最適化 条件: \(-1 < x_1 < 1\) \(-1 < x_2 < 1\)

2.7.2. 様々な最適化のレビュー

2.7.2.1. 手始めに: 1次元最適化

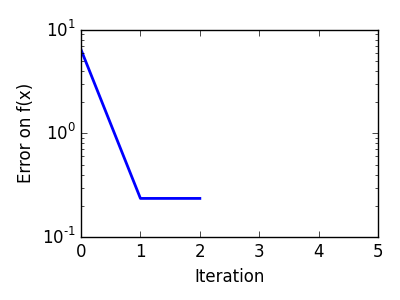
1次元関数を最適化するのに scipy.optimize.brent() を利用します。この方法は囲い込み戦略と二次近似を組み合わせています。

二次関数への Brent 法： 3回の反復で収束しています、二次近似が厳密になるので。
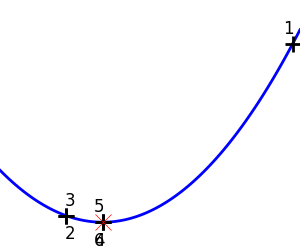非凸関数への Brent 法: 最適化で局所最小値を避けられるかは運の問題であることに注意。

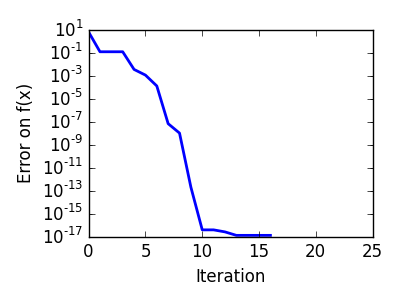>>> from scipy import optimize
>>> def f(x):
...     return -np.exp(-(x - .7)**2)
>>> x_min = optimize.brent(f)  # It actually converges in 9 iterations!
>>> x_min 
0.699999999...
>>> x_min - .7 
-2.1605...e-10

注釈

Brent 法は scipy.optimize.fminbound() を利用して 拘束条件が区間で与えられる 場合にも利用できます

注釈

scipy 0.11 では scipy.optimize.minimize_scalar() は1次元のスカラー最適化の汎用インターフェースを与えます。

2.7.2.2. 勾配に基づく方法

2.7.2.2.1. 勾配降下についての直感

ここではコードではなく 直感 に焦点をあてます。コードはあとからついてきます。

Gradient descent は基本的に、勾配の方向、つまり 最も急な 方向に向かって小さく進んでいきます。

固定ステップでの勾配降下

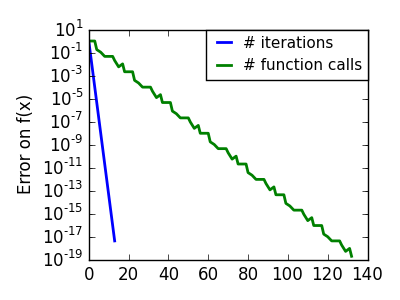
良条件な二次関数。
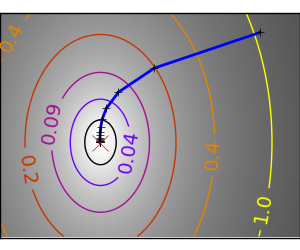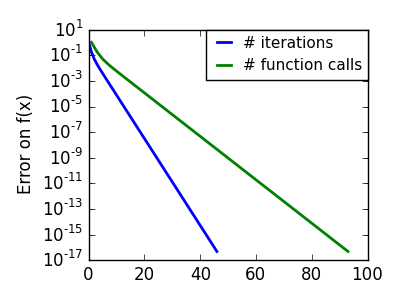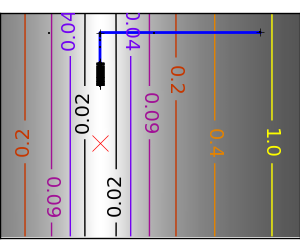
悪条件な二次関数。 悪条件化での勾配法の主な問題は、勾配が最小の方向にいきづらいことです。

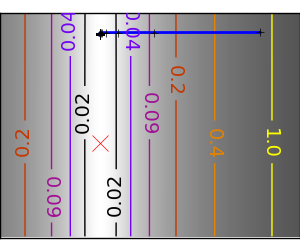異方性が強い (ill-conditionned) 関数は最適化が難しいことがわかります。

知っておいてほしいこと: 条件数と前処理

変数の自然なスケーリング方法がわかっているなら、前もってスケールして相似して振る舞うようにしましょう。これは preconditioning に関連しています。

同様に大きくステップをとることも有利に働く可能性があります。これは勾配降下法のコードでは line search を利用して行なわれます。

勾配降下での適応的なステップ

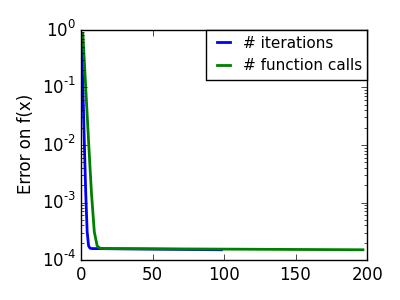
良条件の二次関数。
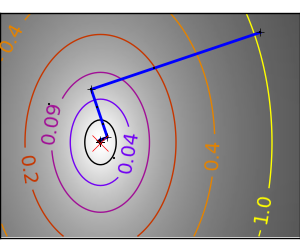悪条件の二次関数。
悪条件な非二次関数
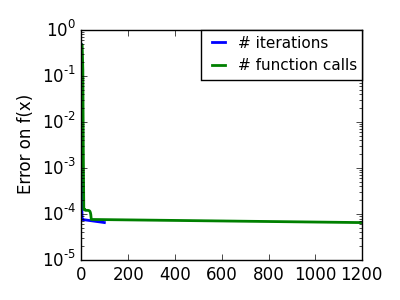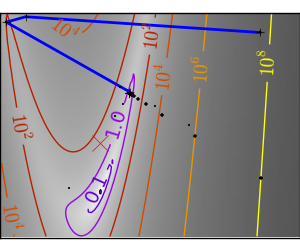
悪条件で二次関数からかけ離れた関数。

関数が二次関数に近い(等高線が楕円な)法が最適化が簡単です。

2.7.2.2.2. 共役勾配法

上に挙げた勾配降下アルゴリズムはおもちゃで実際の問題には利用されません。

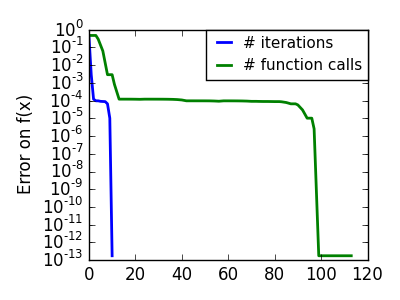
上の実験でみたように、単純な勾配降下アルゴリズムの1つの問題は、勾配の方向に沿って進む度に谷を渡ってしまい、谷をまたいで振動する可能性があることです。共役勾配法は 摩擦 項を加えることでこの問題を解決します: 各ステップは勾配の前2つの値に依存するようになり、急な回り道が減ります。

共役勾配降下

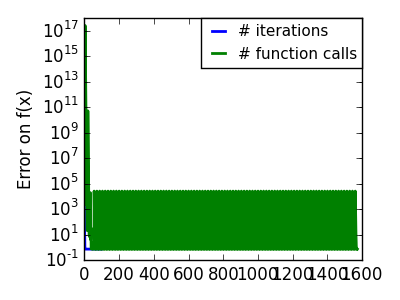
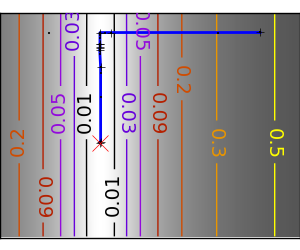
悪条件な非二次関数
悪条件で二次関数からかけ離れた関数。

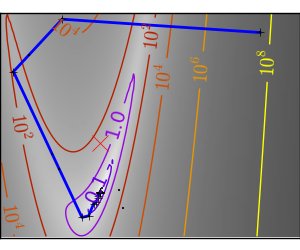共役勾配に基づく手法は scipy では ‘cg’ をつけられます。単純な共役勾配法による関数の最適化は scipy.optimize.fmin_cg() です。

>>> def f(x):   # The rosenbrock function
...     return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> optimize.fmin_cg(f, [2, 2])    
Optimization terminated successfully.
        Current function value: 0.000000
        Iterations: 13
        Function evaluations: 120
        Gradient evaluations: 30
array([ 0.99998968,  0.99997855])

これらの方法は関数の勾配を求める必要があります。これらは計算で求めることもできますが、勾配を渡した方がパフォーマンスよく動きます:

>>> def fprime(x):
...     return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2)))
>>> optimize.fmin_cg(f, [2, 2], fprime=fprime)    
Optimization terminated successfully.
        Current function value: 0.000000
        Iterations: 13
        Function evaluations: 30
        Gradient evaluations: 30
array([ 0.99999199,  0.99998336])

関数が 30回評価されただけなのに対し、勾配なしでは 120 回なことに注意してください。

2.7.2.3. Newton 法と準 Newton 法

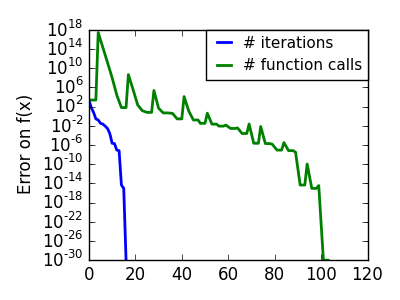
2.7.2.3.1. Newton 法: Hessian (2階微分) を利用

Newton methods はジャンプ方向の計算に局所二次近似を利用します。そのため2つの微分、関数の1階微分: 勾配と Hessian に依存します。

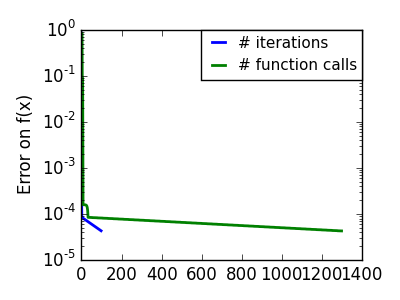
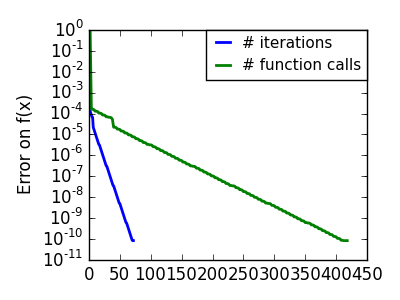
悪条件な二次関数: 二次近似が厳密なので Newton 法がとんでもなく高速です
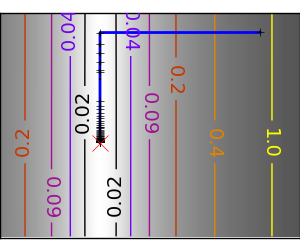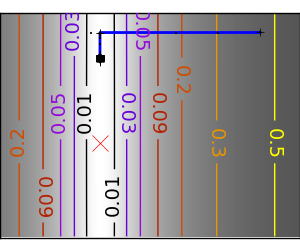
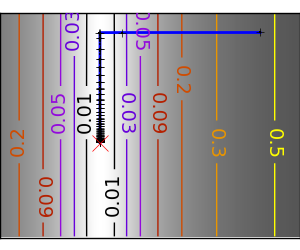
悪条件な非二次関数: ここでは Gauss 関数を最適化します、この関数は二次近似に常に従います。結果として Newton 法はオーバーシュートして振動します。
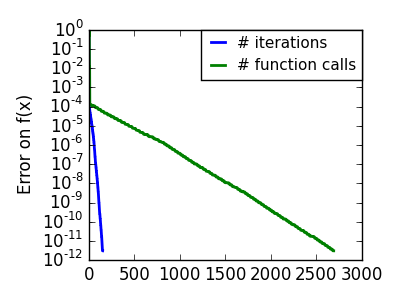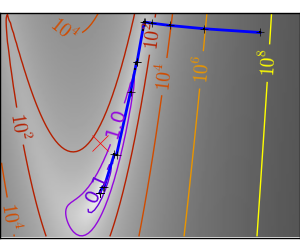
悪条件で二次関数からひどく外れた関数:

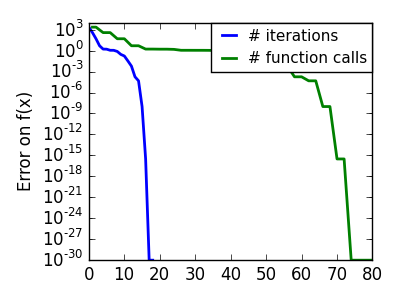scipy では Newton 法による最適化は :fun:`scipy.optimize.fmin_ncg` で実装されています (ここで cg がついているのは内積演算、Hessian の逆行列計算が、共役勾配で実行されていることによります。) scipy.optimize.fmin_tnc() は拘束条件つきの問題にも利用できますがそれほど万能とはいえません:

>>> def f(x):   # The rosenbrock function
...     return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> def fprime(x):
...     return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2)))
>>> optimize.fmin_ncg(f, [2, 2], fprime=fprime)    
Optimization terminated successfully.
        Current function value: 0.000000
        Iterations: 9
        Function evaluations: 11
        Gradient evaluations: 51
        Hessian evaluations: 0
array([ 1.,  1.])

(上の)共益勾配と比較すると、Newton 法は関数の評価回数は少なくすみますが、勾配の評価回数は Hessian の近似に使うために増えます。Hessian をアルゴリズムに渡して計算しましょう:

>>> def hessian(x): # Computed with sympy
...     return np.array(((1 - 4*x[1] + 12*x[0]**2, -4*x[0]), (-4*x[0], 2)))
>>> optimize.fmin_ncg(f, [2, 2], fprime=fprime, fhess=hessian)    
Optimization terminated successfully.
        Current function value: 0.000000
        Iterations: 9
        Function evaluations: 11
        Gradient evaluations: 19
        Hessian evaluations: 9
array([ 1.,  1.])

注釈

次元がかなり高くなると、Hessian の逆行列計算はコストが高くつき、加えて不安定になります(250以上の規模で)。

注釈

Newton 法による最適化は、同じ原理に基づく Newton の求根法 scipy.optimize.newton() と混同しないようにしましょう。

2.7.2.3.2. 準 Newton 法: オンザフライでの Hessian 近似

BFGS: BFGS (Broyden-Fletcher-Goldfarb-Shanno アルゴリズム) は各ステップでの Hessian の近似を改良します。

悪条件な二次関数: 厳密な二次関数では BFGS は Newton 法より速くありませんが、それでも十分高速です。
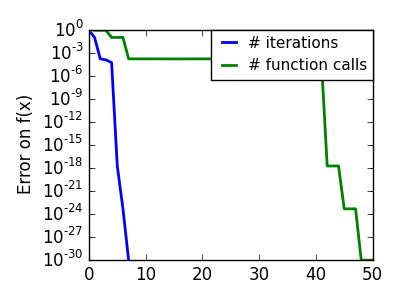悪条件な非二次関数: この例では BFGS は Newton 法よりよい結果を出します、BFGS による曲率の実験的な推定は Hessian よりいいために。
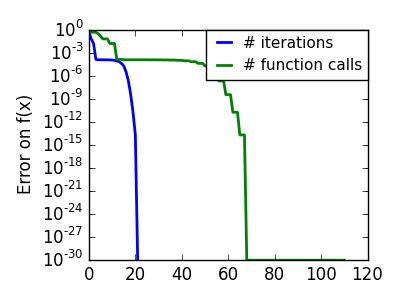悪条件で二次関数からひどく外れた関数:

>>> def f(x):   # The rosenbrock function
...     return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> def fprime(x):
...     return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2)))
>>> optimize.fmin_bfgs(f, [2, 2], fprime=fprime)
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 16
         Function evaluations: 24
         Gradient evaluations: 24
array([ 1.00000017,  1.00000026])

L-BFGS: Limited-memory BFGS は BFGS と共役勾配の中間に位置します: 高い次元 (> 250) では Hessian 行列の計算とその逆行列を求めるコストはとても高くつきます。 L-BFGS は低い位数のものを保持します。さらに scipy では scipy.optimize.fmin_l_bfgs_b() で箱型の境界の扱いも含みます:

>>> def f(x):   # The rosenbrock function
...     return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> def fprime(x):
...     return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2)))
>>> optimize.fmin_l_bfgs_b(f, [2, 2], fprime=fprime)    
(array([ 1.00000005,  1.00000009]), 1.4417677473011859e-15, {...})

注釈

L-BFGS ソルバーで勾配を指定しない場合は approx_grad=1 を追加する必要があります

2.7.2.4. 勾配を必要としない最適化法

2.7.2.4.1. シューティング法: Powell アルゴリズム

ほとんど勾配を利用したアプローチに近い

悪条件な二次関数: Powell 法は低い次元での局所的な悪条件に影響しづらい。
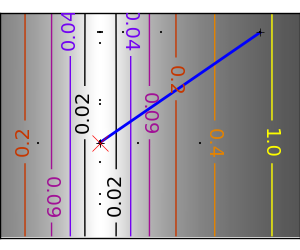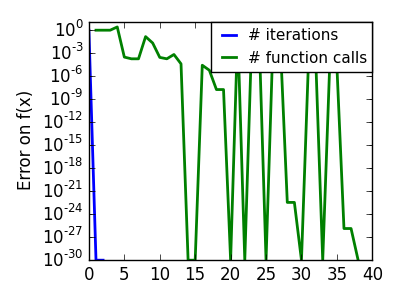悪条件で二次関数からひどく外れた関数:

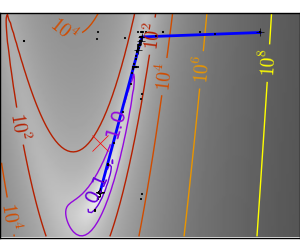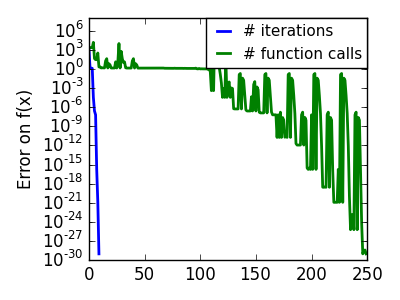2.7.2.4.2. シンプレックス法: Nelder-Mead

Needer-Mead アルゴリズムは高次元空間に対して二分法一般化したアプローチですアルゴリズムは simplex を改良し、最小値を囲い込むために、高次元空間に対して区間や角度を一般化します。

強調すべき点 この方法は勾配を計算しないため、ノイズに対して頑健です。同様に関数が関数が大きなスケールで釣鐘形に見える限りは、実験でのデータ点のように、局所的に滑らかでない場合にも動作します。しかし、滑らかでノイズを含まない関数に対しての勾配法より低速になります。

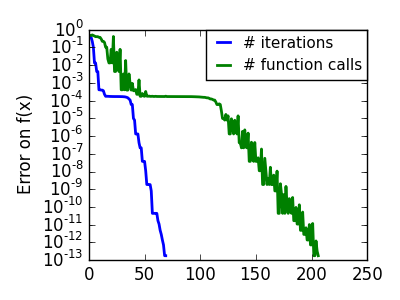
悪条件な非二次関数:
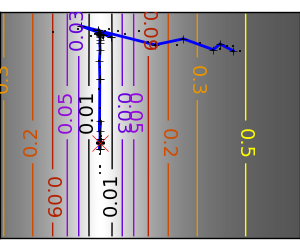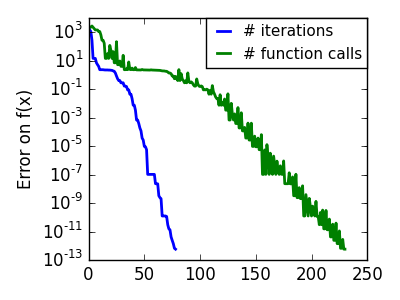
悪条件で二次関数からひどく外れた関数:

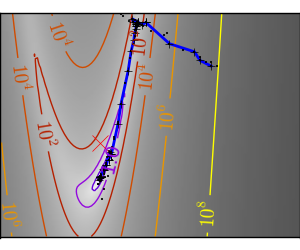scipy では scipy.optimize.fmin() が Nelder-Mead のアプローチを実装します:

>>> def f(x):   # The rosenbrock function
...     return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> optimize.fmin(f, [2, 2])
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 46
         Function evaluations: 91
array([ 0.99998568,  0.99996682])

2.7.2.5. 大域的な最適化

もし問題が唯一の局所最小値 (関数が凸でない限りそれを検証することは困難です) を許容せず、解に近い最適化の初期点の情報を前もって持っていない場合、大域的な最適化が必要です。

2.7.2.5.1. ブルートフォース: グリッド探索

scipy.optimize.brute() は与えられたパラメーターグリッドで関数を評価し、最小値に対応するパラメータを返します。パラメータは numpy.mgrid で与えた範囲で指定されます。デフォルトで各方向に 20 進めます:

>>> def f(x):   # The rosenbrock function
...     return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2
>>> optimize.brute(f, ((-1, 2), (-1, 2)))
array([ 1.00001462,  1.00001547])

2.7.3. scipy での実践的な最適化のためのガイド

2.7.3.1. 手法の選択

Without knowledge of the gradient:  

• 一般的には、数値的に勾配を近似する必要がある場合でも、BFGS (scipy.optimize.fmin_bfgs()) や L-BFGS (scipy.optimize.fmin_l_bfgs_b()) が好ましいです、

• 良条件下では Powell (scipy.optimize.fmin_powell()) や Nelder-Mead (scipy.optimize.fmin()) の両者は勾配を必要とせず高次元でもうまく動きますが悪条件の問題ではこれらは挫折します。

With knowledge of the gradient:  

• BFGS (scipy.optimize.fmin_bfgs()) または L-BFGS (scipy.optimize.fmin_l_bfgs_b()).

• BFGS の計算オーバーヘッドは L-BFGS より大きく、L-BFGS は共役勾配法よりも大きくなります。一方で BFGS たいていの場合で CG と比べて少ない関数評価で済みます。なので共役勾配法は関数の計算コストが低い場合には BFGS よりよい方法といえます。

With the Hessian:  

• Hessian を計算できるなら、Newton 法 (scipy.optimize.fmin_ncg()) が好ましいです。

If you have noisy measurements:  

• Nelder-Mead (scipy.optimize.fmin()) か Powell (scipy.optimize.fmin_powell()) を使いましょう。

2.7.3.2. 最適化を高速化する

• 正しい手法を選択しましょう(上記参照)、可能なら勾配や Hessian が解析的に計算してみましょう。

• preconditionning ができるなら、利用しましょう。

• 初期値を賢く選択しましょう。例えば、多くの似たような最適化をするなら、別の結果でウォームアップした点から始めましょう。

• 精度が必要なければ許容誤差を緩めましょう

2.7.3.3. 勾配の計算

勾配の計算、さらには Hessian の計算、はうんざりする作業ですが、苦労する分の価値があります。 Sympy による記号計算はお手軽にしてくれるかもしれません。

警告

非常に よくある最適化が収束しない原因は、勾配の計算でのヒューマンエラーです。 scipy.optimize.check_grad() を利用して勾配が正しいかを確認できます。この関数は与えた勾配と数値的に計算した勾配の差のノルムを返します:

>>> optimize.check_grad(f, fprime, [2, 2])
2.384185791015625e-07

間違いを見つけるために scipy.optimize.approx_fprime() も見ておきましょう。

2.7.3.4. 人工的な練習問題

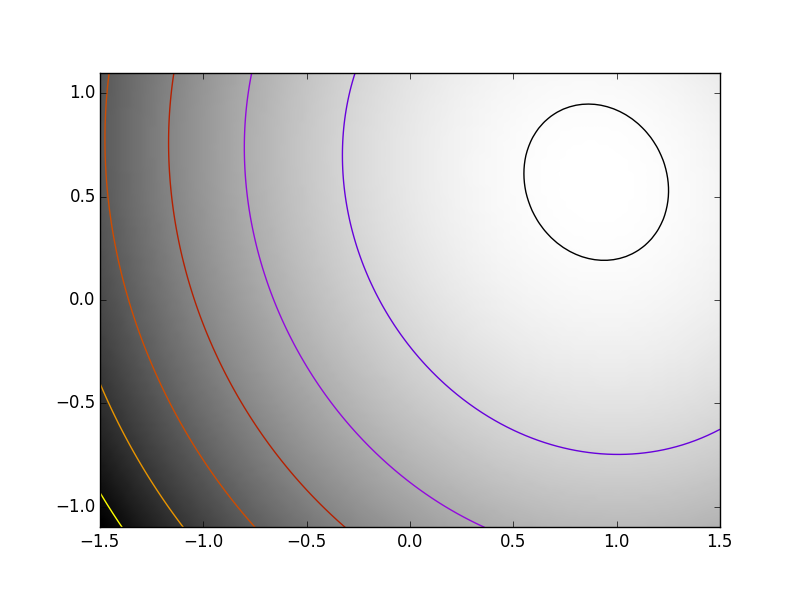
練習問題: 単純(?)な二次関数

以下の関数を K[0] を開始点として最適化しましょう:

np.random.seed(0)
K = np.random.normal(size=(100, 100))

def f(x):
    return np.sum((np.dot(K, x - 1))**2) + np.sum(x**2)**2

時間計測してみましょう。最も高速な方法は? BFGS はどうしてうまく動作しないのでしょうか?

練習問題: 局所的に平らな最小値

関数 exp(-1/(.1*x**2 + y**2) を考えましょう。この関数は (0, 0) で最小となります。 (1, 1) の初期値から始めて、この最小値から 1e-8 となるまで試しましょう。

2.7.4. 特殊例: 非線形最小二乗法

2.7.4.1. ベクトル関数のノルムを最小化する

ベクトル関数のノルムを最小化する最小二乗問題には、特有の構造があり Levenberg–Marquardt algorithm を利用できます、この手法は scipy.optimize.leastsq() で実装されています。

以下のベクトル関数のノルムを最小化してみましょう:

>>> def f(x):
...     return np.arctan(x) - np.arctan(np.linspace(0, 1, len(x)))

>>> x0 = np.zeros(10)
>>> optimize.leastsq(f, x0)
(array([ 0.        ,  0.11111111,  0.22222222,  0.33333333,  0.44444444,
        0.55555556,  0.66666667,  0.77777778,  0.88888889,  1.        ]), 2)

67回関数評価しています(‘full_output=1’ で確認しましょう)。ノルム自体を計算し、一般的な問題に対して良い結果を与える最適化手法 (BFGS) を利用するとどうなりますか:

>>> def g(x):
...     return np.sum(f(x)**2)
>>> optimize.fmin_bfgs(g, x0)   
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 11
         Function evaluations: 144
         Gradient evaluations: 12
array([ -7.4...-09,   1.1...e-01,   2.2...e-01,
         3.3...e-01,   4.4...e-01,   5.5...e-01,
         6.6...e-01,   7.7...e-01,   8.8...e-01,
         1.0...e+00])

BFGS はより多くの関数呼び出しがかかり、結果の精度もよくありません。

注釈

leastsq は BFGS と比べて、出力ベクトルの次元が最適化のパラメータの数に比べて大きいときに、うまく動きます。

警告

関数が線形の場合には、線形代数の問題となるので scipy.linalg.lstsq() を利用して解くべきです。

2.7.4.2. 曲線のフィッティング

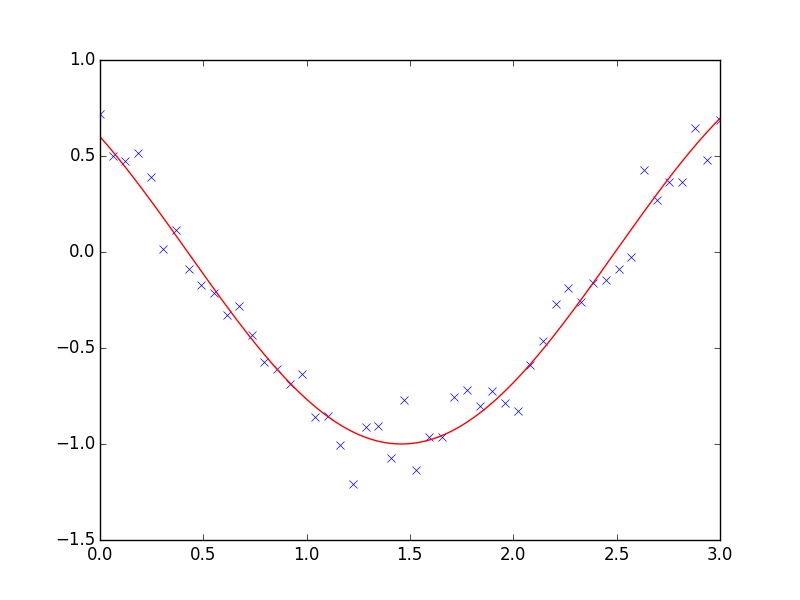
最小二乗問題はデータが非線形な場合にしばしば遭遇します。一方で最適化手問題を自身で構築することも可能です、scipy はそのためのヘルパー関数として scipy.optimize.curve_fit() を提供しています:

>>> def f(t, omega, phi):
...     return np.cos(omega * t + phi)

>>> x = np.linspace(0, 3, 50)
>>> y = f(x, 1.5, 1) + .1*np.random.normal(size=50)

>>> optimize.curve_fit(f, x, y)
(array([ 1.51854577,  0.92665541]), array([[ 0.00037994, -0.00056796],
       [-0.00056796,  0.00123978]]))

練習問題

同じことを omega = 3 でやってみましょう。何が難しくしているのでしょうか?

2.7.5. 拘束条件付きの最適化

2.7.5.1. 箱型の境界

箱型の境界は最適化対象のパラメータそれぞれを制限することに対応します。いくつかの問題では、箱型境界でない元々の問題を変数を変更して書き直すことができます。

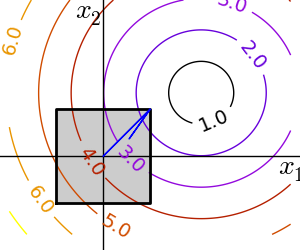
• 1次元最適化では scipy.optimize.fminbound()

• scipy.optimize.fmin_l_bfgs_b() は境界拘束条件つきの quasi-Newton 法:

  >>> def f(x):
  ...    return np.sqrt((x[0] - 3)**2 + (x[1] - 2)**2)
  >>> optimize.fmin_l_bfgs_b(f, np.array([0, 0]), approx_grad=1, bounds=((-1.5, 1.5), (-1.5, 1.5)))   
  (array([ 1.5,  1.5]), 1.5811388300841898, {...})
  

2.7.5.2. 一般的な拘束条件

関数で指定される等式と不等式で指定される拘束条件: f(x) = 0 や g(x)< 0 。

• scipy.optimize.fmin_slsqp() は連続的な最小二乗法プログラミング: 等式及び不等式の拘束条件に: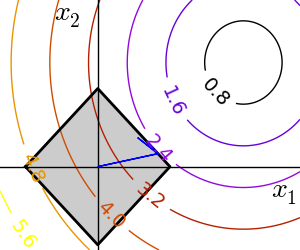

  

  >>> def f(x):
  ...     return np.sqrt((x[0] - 3)**2 + (x[1] - 2)**2)
  
  >>> def constraint(x):
  ...     return np.atleast_1d(1.5 - np.sum(np.abs(x)))
  
  >>> optimize.fmin_slsqp(f, np.array([0, 0]), ieqcons=[constraint, ])
  Optimization terminated successfully.    (Exit mode 0)
              Current function value: 2.47487373504
              Iterations: 5
              Function evaluations: 20
              Gradient evaluations: 5
  array([ 1.25004696,  0.24995304])
  

• scipy.optimize.fmin_cobyla() 線形近似による拘束条件つき最適化: 不等式の拘束条件のみ:

  >>> optimize.fmin_cobyla(f, np.array([0, 0]), cons=constraint)
  array([ 1.25009622,  0.24990378])
  

警告

上記の問題は Lasso 問題として統計で知られており、このための効率的な方法が知られています(例えば scikit-learn にあります)。特化した解法がある場合は一般的なソルバーは利用しないようにしましょう。

Lagrange 未定乗数

少しばかり数学をやる用意があれば、多くの拘束条件つきの最適化問題は拘束条件なしの最適化問題に Lagrange multipliers として知られる数学的手法を利用することで変換できます。