3.5. Mayavi による 3D プロット¶

著者: Gaël Varoquaux
ちなみに
Mayavi は対話的な3次元プロットパッケージです。 matplotlib も簡単な3次元プロットを持っていますが、 Mayavi はより強力なエンジン ( VTK ) を利用し、大規模なデータや複雑なデータを表示するのに向いています。
章の内容
3.5.1. Mlab: スクリプトインターフェース¶
mayavi.mlab モジュールは matplotlib や matlab の作図インターフェースと同様に numpy array に適用するシンプルなプロット機能を提供します。IPython を --gui=wx スイッチ付きで起動して試してみて下さい、
3.5.1.1. 3D プロット関数¶
3.5.1.1.1. 点¶
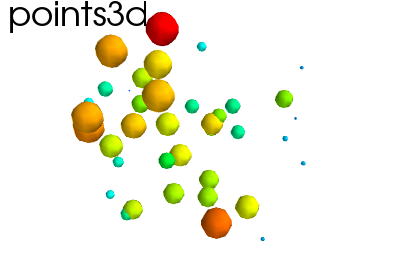
ヒント
3次元での点、marker (もしくは “glyphs”) で表わされ、オプションとして異なるサイズ
x, y, z, value = np.random.random((4, 40))
mlab.points3d(x, y, z, value)
3.5.1.1.2. 線¶
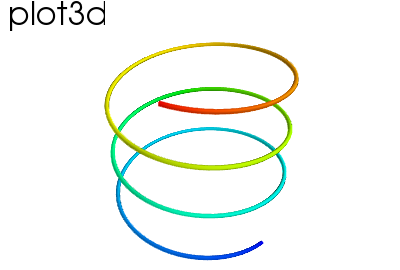
ヒント
3次元で点をつなげた線、オプションとして太さや色の変化。
mlab.clf() # Clear the figure
t = np.linspace(0, 20, 200)
mlab.plot3d(np.sin(t), np.cos(t), 0.1*t, t)
3.5.1.1.3. 立体表面¶
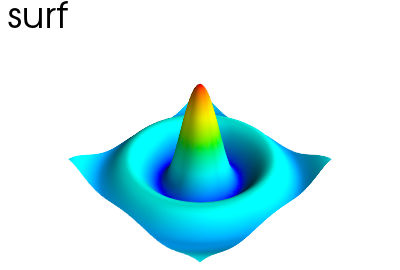
ヒント
表面は等高線を2次元配列で表現し与えます
mlab.clf()
x, y = np.mgrid[-10:10:100j, -10:10:100j]
r = np.sqrt(x**2 + y**2)
z = np.sin(r)/r
mlab.surf(z, warp_scale='auto')
3.5.1.1.4. 任意の regular mesh¶
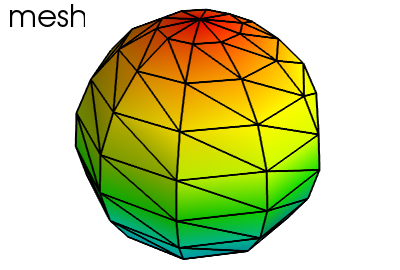
ヒント
表面のメッシュは各ノード点の位置を x, y, z で渡します
mlab.clf()
phi, theta = np.mgrid[0:np.pi:11j, 0:2*np.pi:11j]
x = np.sin(phi) * np.cos(theta)
y = np.sin(phi) * np.sin(theta)
z = np.cos(phi)
mlab.mesh(x, y, z)
mlab.mesh(x, y, z, representation='wireframe', color=(0, 0, 0))
注釈
表面は 連結された 点で定義され、三角形や多角形を形成します。mayavi.mlab.surf() と mayavu.mlab.mesh() では接続は配列のレイアウトに応じて暗黙に与えられます。 mlab.triangler_mesh() についても参照して下さい。
私達のデータはしばしば点と値だけではありません、いくつかの connectivity の情報を必要とします
3.5.1.1.5. 体積データ¶

ヒント
データが3次元で 密 な場合、より表示が困難になります。対処の1つはデータの等高面を表示することです。
mlab.clf()
x, y, z = np.mgrid[-5:5:64j, -5:5:64j, -5:5:64j]
values = x*x*0.5 + y*y + z*z*2.0
mlab.contour3d(values)
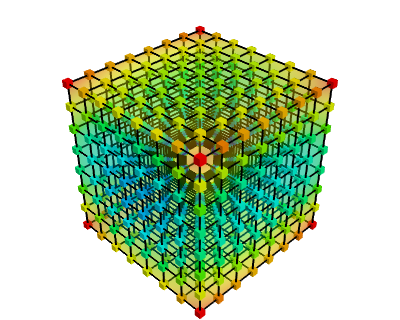
この関数は正方格子で動作します value 配列は3次元配列で格子の形状を与えます。
3.5.1.2. 図と装飾¶
3.5.1.2.1. 図の管理¶
ちなみに
表示している図を制御するのに便利な関数の一覧
現在の図を取得: |
mlab.gcf() |
現在の図を消去する: |
mlab.clf() |
現在の図を設定する: |
mlab.figure(1, bgcolor=(1, 1, 1), fgcolor=(0.5, 0.5, 0.5) |
図を画像ファイルに保存する: |
mlab.savefig(‘foo.png’, size=(300, 300)) |
視点を変更する |
mlab.view(azimuth=45, elevation=54, distance=1.) |
3.5.1.2.2. 作図のプロパティを変更する¶
ちなみに
図の中の様々なオブジェクトの多くのプロパティが変更できます。これらの visualization が mlab 関数で作成されている場合、これらの関数のキーワード引数を使うのが最も簡単な方法です、やり方はドキュメンテーション文字列にあります。
docstring の例: mlab.mesh
2次元配列として与えられた、格子状に並んだデータを表面として作図しましょう.
関数の特徴:
mesh(x, y, z, ...)
x, y, z は2次元配列で全て同じシェイプで表面の頂点を与えます. これらの点の連結は配列上での連結を意味します.
単純な構造(直交格子のような)は surf 関数を使うとよいでしょう、surf 関数はより効率的なデータ構造を作成します。
キーワード引数:
color: vtk オブジェクトの色。与えられた場合、カラーマップを上書きします。この引数が0から1までの範囲の浮動小数点数の3つ組みで与えます、例 白として (1,1,1) を与える。
colormap: 使うカラーマップのタイプ
extent: [xmin, xmax, ymin, ymax, zmin, zmax] デフォルトでは x, y, x の配列の範囲です. 作成されるオブジェクトの範囲を変更したいときに利用します.
figure: 移植したい図.
line_width: 線の太さ. 浮動小数点数でなければいけません. デフォルト: 2.0
mask: データの点を減らすためのブーリアン値のマスク配列.
mask_points: 与えられた場合 ‘mask_points’ 外のデータ点だけが表示されます. このオプションは整数か None からなる巨大なデータセットで表示する点を減らすのに便利です.
mode: グリフ glyph のモード. ‘2darrow’, ‘2dcircle’, ‘2dcross’, ‘2ddash’, ‘2ddiamond’, ‘2dhooked_arrow’, ‘2dsquare’, ‘2dthick_arrow’, ‘2dthick_cross’ or ‘2dtriangle’, ‘2dvertex’, ‘arrow’, ‘cone’, ‘cube’ or ‘cylinder’, ‘point’, ‘sphere’ のどれかでなければいけません. デフォルト: sphere
name: 作成される vtk オブジェクトの名前.
representation: 表面の表示のタイブ. ‘surface’, ‘wireframe’, ‘points’, ‘mesh’ or ‘fancymesh’ のどれかでなければいけません. デフォルト: surface
resolution: 作成されるグリフ glyph の解像度例えば sphere に対しては theta と phi の分割数です. 整数でなければいけません. デフォルト: 8
scalars: オプションとして与えることができるスカラーデータ.
scale_factor: fancy_mesh モードでの頂点を表す glyph の縮尺係数. 浮動小数点数でなければいけません. デフォルト: 0.05
scale_mode: グリフ glyph の縮尺モード (‘vector’, ‘scalar’, または ‘none’).
transparent: 数値に応じて actor の透明度を設定します.
tube_radius: mesh モードでの線を表わすためのチューブの半径. None の場合には, 単純な線が使われます.
tube_sides: 線を表わすためのチューブの側面の数. 浮動小数点数でなければいけません. デフォルト: 6
vmax: vmax はカラーマップの目盛に使われます. None の場合, データの最大値が使われます
vmin: vmin はカラーマップの目盛に使われます. None の場合, データの最小値が使われます

例:
In [1]: import numpy as np
In [2]: r, theta = np.mgrid[0:10, -np.pi:np.pi:10j]
In [3]: x = r * np.cos(theta)
In [4]: y = r * np.sin(theta)
In [5]: z = np.sin(r)/r
In [6]: from mayavi import mlab
In [7]: mlab.mesh(x, y, z, colormap='gist_earth', extent=[0, 1, 0, 1, 0, 1])
Out[7]: <mayavi.modules.surface.Surface object at 0xde6f08c>
In [8]: mlab.mesh(x, y, z, extent=[0, 1, 0, 1, 0, 1],
...: representation='wireframe', line_width=1, color=(0.5, 0.5, 0.5))
Out[8]: <mayavi.modules.surface.Surface object at 0xdd6a71c>
3.5.1.2.3. 装飾¶
ちなみに
追加の情報を載せるために様々な要素を図に追加することができます、たとえばカラーバーやタイトルなど。
In [9]: mlab.colorbar(Out[7], orientation='vertical')
Out[9]: <tvtk_classes.scalar_bar_actor.ScalarBarActor object at 0xd897f8c>
In [10]: mlab.title('polar mesh')
Out[10]: <enthought.mayavi.modules.text.Text object at 0xd8ed38c>
In [11]: mlab.outline(Out[7])
Out[11]: <enthought.mayavi.modules.outline.Outline object at 0xdd21b6c>
In [12]: mlab.axes(Out[7])
Out[12]: <enthought.mayavi.modules.axes.Axes object at 0xd2e4bcc>
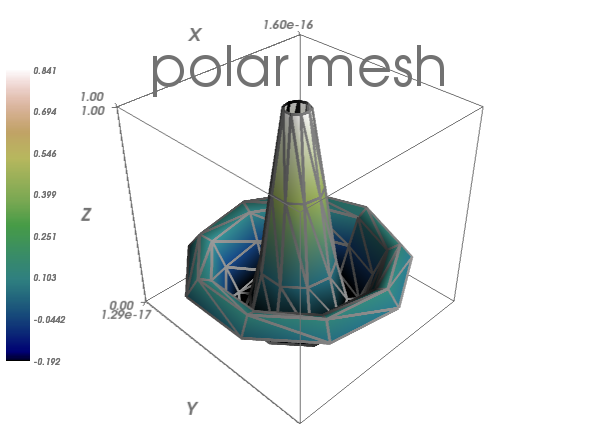
警告
** extent:** plotting オブジェクトに extent を指定した場合 mlab.outline と mlab.axes はデフォルトでそれらを取得しません
3.5.2. 対話的な操作¶
ちなみに
きれいな visualization を Mayavi で作成する最も時間をかけない方法はおそらく対話的に様々な設定で工夫することです。
3.5.2.1. “pipeline dialog”¶
この画面の ‘Mayavi’ ボタンをクリックして, ダイアログでオブジェクトのプロパティを制御できます.
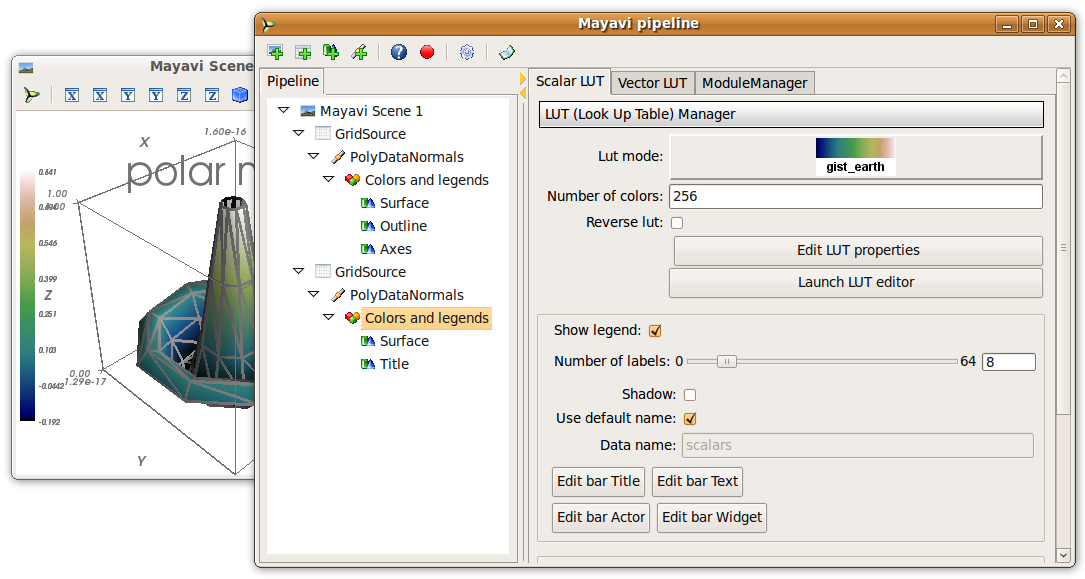
Mayavi Scene ノードで図の背景を設定
Colors and legends ノードでカラーマップを設定
ノードを右クリックしてモジュールやフィルターを追加
3.5.2.2. スクリプト記録ボタン¶
プログラムがそれらを変更するのにどんなコードを利用したかを知るのに利用できます、赤いボタンをクリックしてプロパティを変更すると、コードの対応する行が生成されます。
3.5.3. データの切り出し: ソース、モジュール、フィルター¶
3.5.3.1. 例: 磁場を調べる¶
Helmholtz コイルにより生成された磁場のシミュレーションをしたいとします。 examples/compute_field.py スクリプトが計算をして B 配列を与えます、この配列は (3 x n) で最初の軸は磁場 (Bx, By, Bz) の方向で、2つ目の軸は位置のインデクスを示す数です。配列 X, Y そして Z はこれらのデータ点の位置を与えます。
練習問題
磁場を可視化します。ゴールはシミュレーションのコードが正しいことを確認することです。
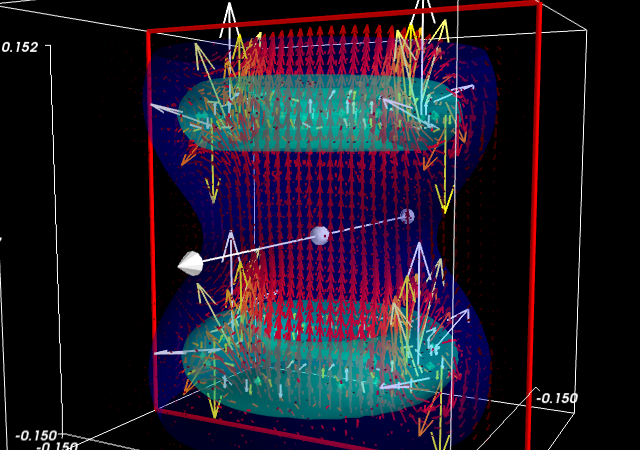
提案
ベクトル場のノルムを計算すれば、等高面を適用できます。
mayavi.mlab.quiver3d()を利用することでベクトルをプロットできます。同様に ‘masking’ オプションを (GUI で)利用することで少し密にプロットできます。
3.5.3.2. データを異なる視点で: ソースとモジュール¶
ちなみに
上で見たように、異なる方法で同じデータをみることは好ましいことでしょう。
Maya の visualization は data source をロードし、次に modules を利用して画面に表示します。
「パイプライン」ビューでこのことを見ることができます。パイプラインのノードを右クリックすることで、新しいモジュールを追加できます。
クイズ
VectorCutPlane をベクトルに追加して mayavi.mlab.quiver3d() を作れないのは何故でしょう?
3.5.3.2.1. 異なるソース: scatter と field¶
ちなみに
データは異なる記述形式でやってきます。
同じ間隔で値が並んだ3次元ブロックは構造化されています: 1回の測定値は他の隣りのものと関連していることや、どうやれば連続的に補間すればいいか簡単にわかるでしょう。このようなデータを field と呼びます、これは物理の用語からの借用で、空間に対して連続に定義されることからです。
ランダムな位置でランダムな並びで測定されたデータ点はわかりにくく補間も悪条件になります: データ構造自身は隣接するデータとの関係を伝えません。このようなデータを scatter と呼びます。
 |
 |
|---|---|
構造化されておらずデータが接続されないデータ: scatter |
構造化されて接続されているデータ: field |
| mlab.points3d, mlab.quiver3d | mlab.contour3d |
scatter に対応するデータソースは mayavi.mlab.pipeline.scalar_scatter() または mayavi.mlab.pipeline.vector_scatter() で作ることができます; field データソースは mlab.pipeline.scalar_field() または mlab.pipeline.vector_field() で作れます。
練習問題:
等高線(例えば磁場のノルム)を作るにはこれらの関数の内どれかを使い、正しい モジュール を GUI ダイアログをクリックして追加します。
正しいソースを作って ‘vector_cut_plane’ を適用し、前に示した磁場の図を再現しましよう。
困難の内の1つはデータを正しい形式 (配列の数、シェイプ)で関数に与えることだということを注意しておきます。現実のデータではよくあります。
参考
ソースについての詳細は Mayavi manual にあります。
3.5.3.2.2. データの変換: フィルタ¶
ベクトル場 を作成した場合、大きさに応じた等高面で可視化したくなるでしょう。しかし等高面モジュールはスカラーデータに対してのみ適用でき、ベクトルデータに対しては適用できません。 filter を使って ExtractVectorNorm でベクトル場にスカラー値を加えることができます。
フィルタはデータを変換し、ソースとモジュールの間に追加することができます。
練習問題
GUI を利用して ExtractVectorNorm フィルタを追加して場の大きさによる等高面を表示しましょう。
3.5.3.2.3. mlab.pipeline: スクリプトレイヤー¶
mlab スクリプティングレイヤーはパイプラインを構築します。これらのパイプラインは mlab.pipeline インターフェースを使い再生産できます: 各ステップは対応する mlab.pipeline 関数 (単純に名前を小文字にしてアンダースコアで分割されて変換された名前: ExtractVectorNorm なら extract_vector_norm) を持ちます。この関数は適用するノードを引数にとり、同様にオプションパラメータをとり、新しいノードを返します。
例えば、磁場の等高面はこのようなコードになります:
mlab.pipeline.iso_surface(mlab.pipeline.extract_vector_norm(field),
contours=[0.1*Bmax, 0.4*Bmax],
opacity=0.5)

練習問題
mlab.pipeline interface を利用することで場の大きさに応じた等高面とベクトルの切断面の完全な visualization を生成できます。
(図をクリックすると解答が得られます。)
3.5.4. データのアニメーション化¶
ちなみに
動画や対話的なアプリケーションを作って、可視化されて表示されたデータを変更したいと思うかもしれません。
mlab プロット関数を利用するか mlab.pipeline 関数で可視化したら、新しい値を mlab_source 属性に新しい値を代入することでデータを更新できます
x , y , z = np.ogrid[-5:5:100j ,-5:5:100j, -5:5:100j]
scalars = np.sin(x * y * z) / (x * y * z)
iso = mlab.contour3d(scalars, transparent=True, contours=[0.5])
for i in range(1, 20):
scalars = np.sin(i * x * y * z) /(x * y * z)
iso.mlab_source.scalars = scalars
参考
より詳しくは Mayavi documentation
イベントループ
ユーザの対話操作のために (例えばマウスで視点を変更する), Mayavi はこれらのイベント処理が必要になります。上の for ループはこの処理を妨害します。Mayavi ドキュメントに詳しい a workaround があります。
3.5.5. 対話的なダイアログの作成¶
Mayavi で対話的なダイアログを作成するのはとても簡単で Traits ライブラリを利用します (これについて扱った章 Traits: 対話ダイアログを作る を参照して下さい)。
3.5.5.1. 単純なダイアログ¶
from traits.api import HasTraits, Instance
from traitsui.api import View, Item, HGroup
from mayavi.core.ui.api import SceneEditor, MlabSceneModel
def curve(n_turns):
"The function creating the x, y, z coordinates needed to plot"
phi = np.linspace(0, 2*np.pi, 2000)
return [np.cos(phi) * (1 + 0.5*np.cos(n_turns*phi)),
np.sin(phi) * (1 + 0.5*np.cos(n_turns*phi)),
0.5*np.sin(n_turns*phi)]
class Visualization(HasTraits):
"The class that contains the dialog"
scene = Instance(MlabSceneModel, ())
def __init__(self):
HasTraits.__init__(self)
x, y, z = curve(n_turns=2)
# Populating our plot
self.plot = self.scene.mlab.plot3d(x, y, z)
# Describe the dialog
view = View(Item('scene', height=300, show_label=False,
editor=SceneEditor()),
HGroup('n_turns'), resizable=True)
# Fire up the dialog
Visualization().configure_traits()
ちなみに
上のコードをちょっと読んでみましょう(examples/mlab_dialog.py) 。
まず curve 関数がプロットしたい曲線の座標を計算するのに利用されます。
次にダイアログが HasTraits を継承したオブジェクトにより定義されます、これは Traits にあるように実施されます。ここで重要なことは Mayavi の scenne がある Traits の属性 (Instance) として追加されていることです。このことはダイアログを埋め込むのに重要です。ダイアログの view はオブジェクトの view と属性として定義されます。このオブジェクトの初期化では曲線の3次元の scene が生成されます。
最後に configure_traits メソッドはダイアログを作成し、イベントループを開始します。
参考
少しだけ Mayavi でダイアログを扱う際に気をつける点があります。 Mayavi documentation を読んでください
3.5.5.2. 対話的にする¶
Traits events handler と mlab_source を組み合わせてダイアログつきで可視化を変更できます。
curve の定義で n_turns パラメータをユーザが変化させることができます。そのためにはこうする必要があります:
n_turns属性を visualization オブジェクトに定義するために、ダイアログに表われるようにします。Range型を利用します。この属性の変更と曲線の再計算を結び付けます。そのために
on_traits_changeデコレータを利用します。
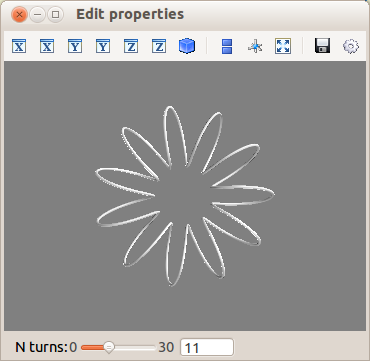
from traits.api import Range, on_trait_change
class Visualization(HasTraits):
n_turns = Range(0, 30, 11)
scene = Instance(MlabSceneModel, ())
def __init__(self):
HasTraits.__init__(self)
x, y, z = curve(self.n_turns)
self.plot = self.scene.mlab.plot3d(x, y, z)
@on_trait_change('n_turns')
def update_plot(self):
x, y, z = curve(self.n_turns)
self.plot.mlab_source.set(x=x, y=y, z=z)
view = View(Item('scene', height=300, show_label=False,
editor=SceneEditor()),
HGroup('n_turns'), resizable=True)
# Fire up the dialog
Visualization().configure_traits()
ちなみに
例についての完全なコード: examples/mlab_dialog.py.
3.5.6. まとめて一緒に¶
練習問題
磁場シミュレーションのコードを利用して、2つのコイルを動かすダイアログを作り: これらのパラメータを変更しましょう。
ヒント: ダイアログの項目を3次元のベクトルで定義するには:
direction = Array(float, value=(0, 0, 1), cols=3, shape=(3,))
Coil Application で270行からなるコイル設計のための本格的なアプリケーションが見られます。
