1.3.4. 高度な演算¶
この節の内容
1.3.4.1. 多項式¶
Numpy は様々な基底での多項式も含んでいます:
例 \(3x^2 + 2x - 1\):
>>> p = np.poly1d([3, 2, -1])
>>> p(0)
-1
>>> p.roots
array([-1. , 0.33333333])
>>> p.order
2
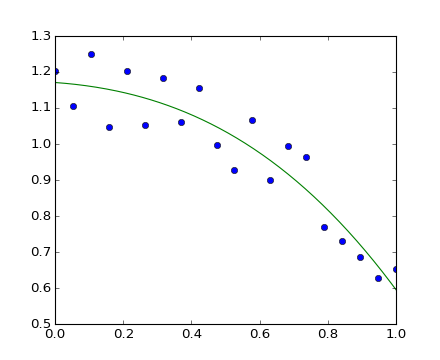
>>> x = np.linspace(0, 1, 20)
>>> y = np.cos(x) + 0.3*np.random.rand(20)
>>> p = np.poly1d(np.polyfit(x, y, 3))
>>> t = np.linspace(0, 1, 200)
>>> plt.plot(x, y, 'o', t, p(t), '-')
[<matplotlib.lines.Line2D object at ...>, <matplotlib.lines.Line2D object at ...>]
より詳しくは http://docs.scipy.org/doc/numpy/reference/routines.polynomials.poly1d.html を参照して下さい。
1.3.4.1.1. さらなる多項式(それ以外の基底)¶
Numpy はさらに洗練された多項式のインターフェースを持っています、それによって Chebyshev 基底のような基底もサポートしています。
\(3x^2 + 2x - 1\):
>>> p = np.polynomial.Polynomial([-1, 2, 3]) # coefs in different order!
>>> p(0)
-1.0
>>> p.roots()
array([-1. , 0.33333333])
>>> p.degree() # In general polynomials do not always expose 'order'
2
Chebyshev 基底を利用した多項式の例として [-1, 1] の範囲での多項式:
>>> x = np.linspace(-1, 1, 2000)
>>> y = np.cos(x) + 0.3*np.random.rand(2000)
>>> p = np.polynomial.Chebyshev.fit(x, y, 90)
>>> t = np.linspace(-1, 1, 200)
>>> plt.plot(x, y, 'r.')
[<matplotlib.lines.Line2D object at ...>]
>>> plt.plot(t, p(t), 'k-', lw=3)
[<matplotlib.lines.Line2D object at ...>]
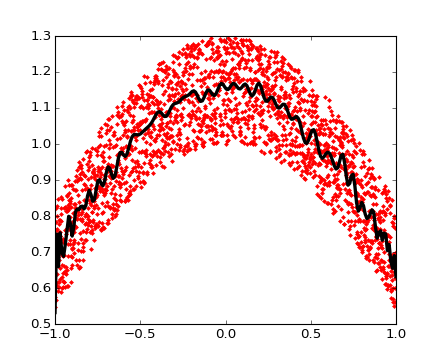
Chebyshev 多項式は補間するのに有利な点をいくつか持っています。
1.3.4.2. データファイルの読み込み¶
1.3.4.2.1. テキストファイル¶
例: populations.txt:
# year hare lynx carrot 1900 30e3 4e3 48300 1901 47.2e3 6.1e3 48200 1902 70.2e3 9.8e3 41500 1903 77.4e3 35.2e3 38200
>>> data = np.loadtxt('data/populations.txt')
>>> data
array([[ 1900., 30000., 4000., 48300.],
[ 1901., 47200., 6100., 48200.],
[ 1902., 70200., 9800., 41500.],
...
>>> np.savetxt('pop2.txt', data)
>>> data2 = np.loadtxt('pop2.txt')
注釈
複雑なテキストファイルを持っている場合はこれを試して下さい:
np.genfromtxtPython の I/O 関数や正規表現を利用してパースする(Python はこの目的にとても向いています)
助言: ファイルシステムを IPython で閲覧する
In [1]: pwd # show current directory
'/home/user/stuff/2011-numpy-tutorial'
In [2]: cd ex
'/home/user/stuff/2011-numpy-tutorial/ex'
In [3]: ls
populations.txt species.txt
1.3.4.2.2. 画像¶
Matplotlib を使って:
>>> img = plt.imread('data/elephant.png')
>>> img.shape, img.dtype
((200, 300, 3), dtype('float32'))
>>> plt.imshow(img)
<matplotlib.image.AxesImage object at ...>
>>> plt.savefig('plot.png')
>>> plt.imsave('red_elephant', img[:,:,0], cmap=plt.cm.gray)
(RGBの) 1チャンネルだけ保存する:
>>> plt.imshow(plt.imread('red_elephant.png'))
<matplotlib.image.AxesImage object at ...>
他のライブラリ:
>>> from scipy.misc import imsave
>>> imsave('tiny_elephant.png', img[::6,::6])
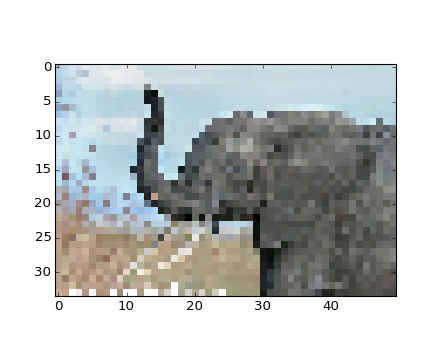
>>> plt.imshow(plt.imread('tiny_elephant.png'), interpolation='nearest')
<matplotlib.image.AxesImage object at ...>
1.3.4.2.3. Numpy の独自フォーマット¶
Numpy は独自のバイナリ形式を持っていて可搬性はありませんが、効率的に I/O を扱えます:
>>> data = np.ones((3, 3))
>>> np.save('pop.npy', data)
>>> data3 = np.load('pop.npy')
1.3.4.2.4. よく知られた(そしてよりわかりにくい)ファイルフォーマット¶
- HDF5: h5py, PyTables
- NetCDF:
scipy.io.netcdf_file, netcdf4-python, ... - Matlab:
scipy.io.loadmat,scipy.io.savemat - MatrixMarket:
scipy.io.mmread,scipy.io.mmwrite - IDL:
scipy.io.readsav
... もし誰かが使っているのなら、おそらくそれを扱う Python ライブラリもあるでしょう。
練習問題: テキストデータファイル
populations.txt からデータを読み込む Python スクリプトを書きましょう:: そして、最後の列と最初の5行を捨てましょう。より小さくなったデータセットを pop2.txt に保存しましょう。
Numpy の内部
Numpy の内部に興味を持ったなら Numpy の先進的な機能 に優れた議論があります。
