1.3.5. 練習問題をいくつか

1.3.5.1. 配列の操作

  1. 2次元配列を作成(直接一つ一つ入力せずに):

    [[1,  6, 11],

     [2,  7, 12],

     [3,  8, 13],

     [4,  9, 14],

     [5, 10, 15]]

    そして、2行目と4行目を含む新しい配列を作成。

  2. この配列の各列を割りましょう:

    >>> import numpy as np

    >>> a = np.arange(25).reshape(5, 5)

    b = np.array([1., 5, 10, 15, 20]) で要素毎に. (ヒント: np.newaxis).

  3. 難しい問題: 乱数([0,1] の範囲の)を要素とする 10 x 3 配列を生成し、各列で 0.5 に近い数字をとってくる。

    • abs と argsort を使って各列で近い j 行を見つけましょう。

    • 数を取り出すのにはファンシーインデックスを使ってみましょう。(ヒント: a[i, j] – i の配列は j に対応する列番号のものを持っています。)

1.3.5.2. 画像操作: 顔をフレーム

アライグマの画像を使って numpy 配列の操作をやってみましょう. scipy はこの画像の2次元配列を scipy.misc.face 関数で提供しています:

>>> from scipy import misc

>>> face = misc.face(gray=True)  # 2D grayscale image

ここに操作によって得られる画像を少しだけ載せておきます：違うカラーマップを使う, 画像を切り取る, 特定の部分を変更する.

../../_images/faces.png

  • pylab の imshow 関数で画像を表示してみましょう.

    >>> import pylab as plt

    >>> face = misc.face(gray=True)

    >>> plt.imshow(face)    

    <matplotlib.image.AxesImage object at 0x...>
  • そうすると顔が擬似カラーで表示されます. カラーマップは

    グレーで表示されます。

    >>> plt.imshow(face, cmap=plt.cm.gray)    

    <matplotlib.image.AxesImage object at 0x...>
  • 中央揃えしたより幅の狭い画像を作ってみましょう: 例として、 : for example,

    画像の境界から 100 ピクセル削ってみましょう. 結果を確認するためには imshow で配列を表示してみましょう.

    >>> crop_face = face[100:-100, 100:-100]
  • を黒いロケットで囲ってみましょう。そのために

    覆いたいピクセルを黒にするために対応するマスクを作ります。顔の中心は (660, 330) にあり、マスクは (y-300)**2 + (x-660)**2 で定義します

    >>> sy, sx = face.shape

    >>> y, x = np.ogrid[0:sy, 0:sx] # x and y indices of pixels

    >>> y.shape, x.shape

    ((768, 1), (1, 1024))

    >>> centerx, centery = (660, 300) # center of the image

    >>> mask = ((y - centery)**2 + (x - centerx)**2) > 230**2 # circle

    そしてマスクに対応する画像ピクセルに 0 を代入します. 構文は平易で直感的です.

    >>> face[mask] = 0

    >>> plt.imshow(face)    

    <matplotlib.image.AxesImage object at 0x...>
  • フォローアップ: この問題の全ての指示を

    face_locket.py then execute this script in IPython with %run face_locket.py.

    円を楕円に変えてみましょう。

1.3.5.3. データの統計

populations.txt のデータ:: 北カナダでの20年分の野うさぎ hare と大山猫 lynx (そして 人参 carrot) の個体数が書かれています:

>>> data = np.loadtxt('data/populations.txt')

>>> year, hares, lynxes, carrots = data.T  # trick: columns to variables



>>> import matplotlib.pyplot as plt

>>> plt.axes([0.2, 0.1, 0.5, 0.8]) 

<matplotlib.axes...Axes object at ...>

>>> plt.plot(year, hares, year, lynxes, year, carrots) 

[<matplotlib.lines.Line2D object at ...>, ...]

>>> plt.legend(('Hare', 'Lynx', 'Carrot'), loc=(1.05, 0.5)) 

<matplotlib.legend.Legend object at ...>

[ソースコード, hires.png, pdf]

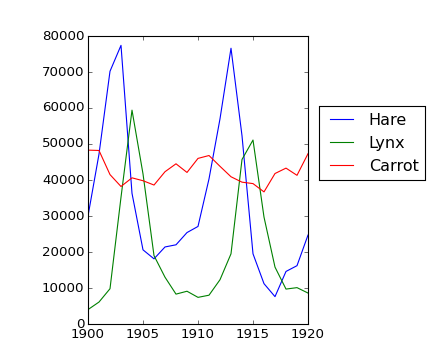
../../_images/numpy_intro_7.png

population.txt のデータに基づいて計算しプリントしましょう...

  1. 各年での各種の個体数の平均と標準偏差。

  2. 各種が最大の個体数になったのは何年。

  3. 各年でどの種が最大の個体数になっていますか。(ヒント: argsort と np.array(['H', 'L', 'C']) のファンシーインデックス)

  4. 個体数が 50000 を越えた年はどの年ですか。(ヒント: 比較と np.any)

  5. 各種の個体数最小になった年のトップ2。(ヒント: argsort とファンシーインデクス)

  6. 野うさぎの個体数変化(help(np.gradient) を参照して下さい)と大山猫の数を比較して(作図して)ください。相関も確認しましょう(help(np.corrcoef) を参照)。

... 全て for ループ無しで。

解答 Python ソースファイル

1.3.5.4. おおざっぱに積分を近似する

\(a^b - c\) を返す関数 f(a, b, c) を書いてください。[0,1] x [0,1] x [0,1] の範囲の値を持つ、24x12x6 の配列を作成して下さい。

近似的に以下の3次元積分を

\[\int_0^1\int_0^1\int_0^1(a^b-c)da\,db\,dc\]

この体積に渡って平均して下さい。厳密な値は: \(\ln 2 - \frac{1}{2}\approx0.1931\ldots\) — 相対誤差はどうですか?

(ヒント: 要素毎の演算とブロードキャストを使ってみて下さい。 np.ogrid を np.ogrid[0:1:20j] のように範囲と点の数を与えて使うことができます。)

助言 Python の関数:

def f(a, b, c):

    return some_result

解答: Python ソースファイル

1.3.5.5. Mandelbrot 集合

[ソースコード, hires.png, pdf]

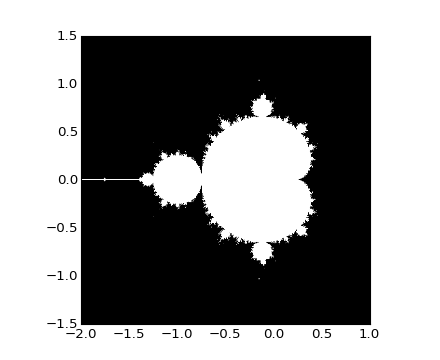
../../_images/2_4_mandelbrot.png

Mandelbrot のフラクタルを計算するスクリプトを書きましょう。Mandelbrot の反復は:

N_max = 50

some_threshold = 50



c = x + 1j*y



for j in xrange(N_max):

    z = z**2 + c

点 (x, y) が \(|c|\) < some_threshold を満す場合、Mandelbrot 集合に属します。

この計算を以下によって行いましょう:

  1. [-2, 1] x [-1.5, 1.5] の範囲の値で格子 c = x + 1j*y の格子を作成しましょう

  2. 反復します

  3. どの点が Mandelbrot 集合に属しているかを示す、2次元の真偽値のマスクを作りましょう

  4. 次のようにして結果を画像として保存します:

>>> import matplotlib.pyplot as plt

>>> plt.imshow(mask.T, extent=[-2, 1, -1.5, 1.5]) 

<matplotlib.image.AxesImage object at ...>

>>> plt.gray()

>>> plt.savefig('mandelbrot.png')

解答: Python ソースコード

1.3.5.6. Markov 連鎖

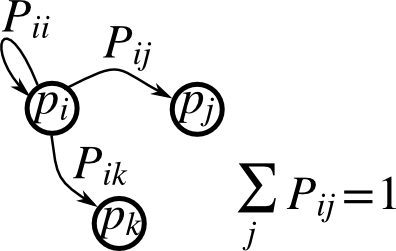
../../_images/markov-chain.png

Markov 連鎖の遷移行列を P、状態の確率分布を p とします:

  1. 0 <= P[i,j] <= 1: 状態 i から 状態 j へ移る確率

  2. 遷移則: \(p_{new} = P^T p_{old}\)

  3. all(sum(P, axis=1) == 1), p.sum() == 1: 規格化

5状態で動作するスクリプトを書き、さらに:

  • ランダム行列を作成し、各列で規格化します。これが遷移行列になります。

  • ランダムな(規格化された)確率分布 p から始めて 50 ステップ勧めて => p_50

  • 定常分布を計算しましょう: P.T の固有値 1(数値的には: 1 に最も近い) の固有ベクトル => p_stationary

固有ベクトルを規格化するのを忘れないようにしましょう — 私は忘れました...

  • p_50 と p_stationary が誤差 1e-5 で等しいことを確認しましょう

ツールボックス: np.random.rand, .dot(), np.linalg.eig, 縮約, abs(), argmin, 比較 all, np.linalg.norm, 等.

解答: Python ソースファイル