>>> import numpy as np

>>> import pylab as pl

>>> from scipy import ndimage

1.5.11.4. 画像処理練習問題解答例: ガラスの中の非融解粒

../../_images/MV_HFV_012.jpg

  1. MV_HFV_012.jpg を開いて表示しましょう. imshow のドキュメンテーション文字列を眺めて右方向 “right” orientation (原点が左下の角になり、普通の配列のように左上の角にない)状態で開きましょう:

    >>> dat = pl.imread('data/MV_HFV_012.jpg')

  2. 測定情報を表示している下のパネル部分を切り取りましょう.

    >>> dat = dat[:-60]

  3. 頻度分布を明確にするために少しだけ中央値フィルターをかけましょう. 頻度分布がどう変化したか調べましょう.

    >>> filtdat = ndimage.median_filter(dat, size=(7,7))

    >>> hi_dat = np.histogram(dat, bins=np.arange(256))

    >>> hi_filtdat = np.histogram(filtdat, bins=np.arange(256))
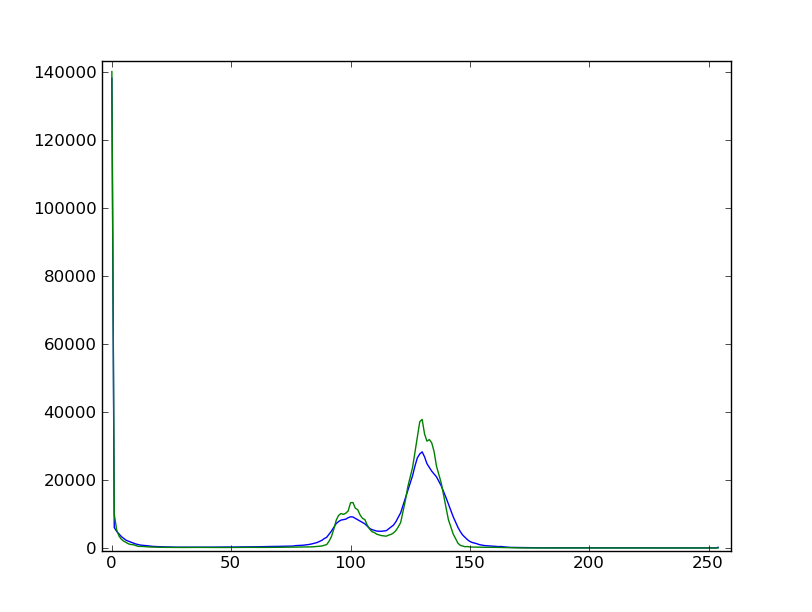
../../_images/exo_histos.png

  1. フィルタした画像の頻度分布を使って, 砂, ガラス, 泡のピクセルのマスクを定義するための閾値を決定しなさい. オプション(宿題): 頻度分布の最小値から閾値を自動的に決定する関数を書きなさい.

    >>> void = filtdat <= 50

    >>> sand = np.logical_and(filtdat > 50, filtdat <= 114)

    >>> glass = filtdat > 114

  2. 3つの相を異なる色で表示しなさい.

    >>> phases = void.astype(np.int) + 2*glass.astype(np.int) + 3*sand.astype(np.int)
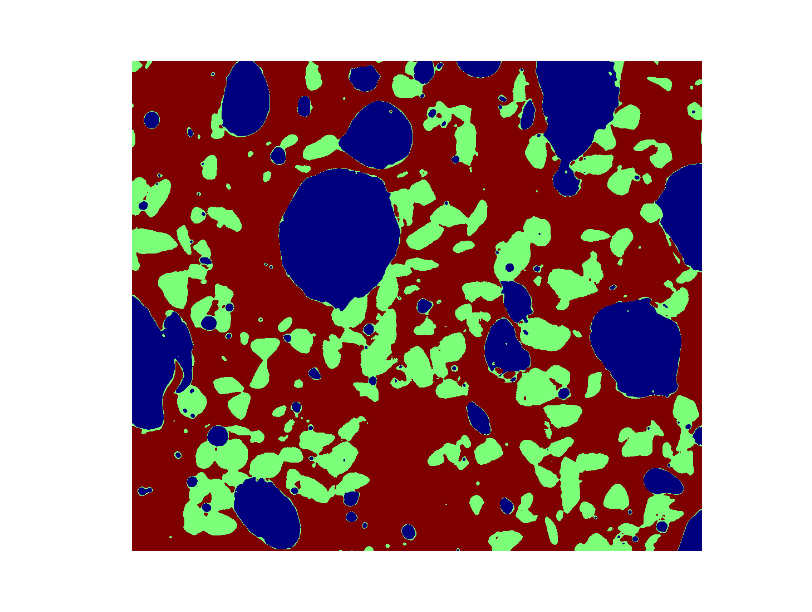
../../_images/three_phases.png

  1. 異なる相のごみをとるために数理形態学を使いなさい.

    >>> sand_op = ndimage.binary_opening(sand, iterations=2)

  2. 全ての泡と砂粒にラベルをつけ, そして10ピクセルより小さい砂粒のマスクを取り除きなさい. そうしたら, ndimage.sum か np.bincount を使って粒の大きさを計算しなさい.

    >>> sand_labels, sand_nb = ndimage.label(sand_op)

    >>> sand_areas = np.array(ndimage.sum(sand_op, sand_labels, np.arange(sand_labels.max()+1)))

    >>> mask = sand_areas > 100

    >>> remove_small_sand = mask[sand_labels.ravel()].reshape(sand_labels.shape)
../../_images/sands.png

  1. 泡の平均的大きさを計算しなさい.

    >>> bubbles_labels, bubbles_nb = ndimage.label(void)

    >>> bubbles_areas = np.bincount(bubbles_labels.ravel())[1:]

    >>> mean_bubble_size = bubbles_areas.mean()

    >>> median_bubble_size = np.median(bubbles_areas)

    >>> mean_bubble_size, median_bubble_size

    (1699.875, 65.0)