1.5. Scipy: 高水準の科学技術計算¶

著者: Adrien Chauve, Andre Espaze, Emmanuelle Gouillart, Gaël Varoquaux, Ralf Gommers

Scipy

scipy パッケージは科学技術計算での共通の問題のための多様なツールボックスがあります。サブモジュール毎に応用範囲が異なっています。応用範囲は例えば、補完、積分、最適化、画像処理、統計、特殊関数等。

scipy は GSL (GNU Scientific Library for C and C++) や Matlab のツールボックスのような他の標準的な科学技術計算ライブラリと比較されます。 scipy は Python での科学技術計算ルーチンの中核となるパッケージです; これは numpy の配列を効率良く扱っているということで、numpy と scipy は密接に協力して動作しています。

ルーチンを実装する前に、望んでいるデータ処理が Scipy で既に実装されているかを確認した方がいいでしょう。プロフェッショナルでないプログラマや科学者は 車輪の再開発 をしたがります、これはバグが多く最適でなく、共有が難しく、メンテナンスできないコードに陥りがちです。対照的に Scipy のルーチンは最適化され、テストされていてるので、利用できるときには利用すべきです。

章の内容

警告

このチュートリアルは決して数値計算の入門ではありません. scipy のサブモジュールと関数を列挙していくことはとても退屈なものになるでしょうから, 代わりに scipy を科学技術計算のためにどう使えばいいか理解するためのいくつかの例を集中して扱います,

scipy は主に特定の作業向けのサブモジュールから構成されています:

`scipy.cluster`	ベクトル量子化 / K 平均法
`scipy.constants`	物理数学定数
`scipy.fftpack`	Fourier 変換
`scipy.integrate`	積分ルーチン
`scipy.interpolate`	補間
`scipy.io`	データ入出力
`scipy.linalg`	線形代数ルーチン
`scipy.ndimage`	n-次元画像パッケージ
`scipy.odr`	直交距離回帰
`scipy.optimize`	最適化
`scipy.signal`	信号処理
`scipy.sparse`	疎行列
`scipy.spatial`	空間データ構造とアルゴリズム
`scipy.special`	任意の数学特殊関数
`scipy.stats`	統計

ちなみに

これらは全て :mod:`numpy`に依存していますが、それぞれはほぼ独立しています。は Numpy とこれらの Scipy モジュールをインポートするのが標準的です。

>>> importnumpyasnp
>>> fromscipyimportstats# same for other sub-modules

本題である scipy の名前空間のほとんどは実質的に numpy の関数となっている関数を含んでいます(scipy.cos is np.cos を試してみてください)。これらは単に歴史的な理由によるものです; そのため、コードの中で import scipy する必要はほとんどの場合でありません。

1.5.1. ファイル入出力: `scipy.io`¶

matlab ファイルの読み込みと保存:

>>> fromscipyimportioasspio
>>> a=np.ones((3,3))
>>> spio.savemat('file.mat',{'a':a})# savemat expects a dictionary
>>> data=spio.loadmat('file.mat',struct_as_record=True)
>>> data['a']
array([[ 1.,  1.,  1.],
       [ 1.,  1.,  1.],
       [ 1.,  1.,  1.]])

画像の読み込み:

>>> fromscipyimportmisc
>>> misc.imread('fname.png')
array(...)
>>> # Matplotlib also has a similar function
>>> importmatplotlib.pyplotasplt
>>> plt.imread('fname.png')
array(...)

さらに:

テキストファイルを読み込む: numpy.loadtxt()/numpy.savetxt()

テキストや csv ファイルを賢く読み込む: numpy.genfromtxt()/numpy.recfromcsv()

高速で効率的ですが、numpy に限定的な、バイナリフォーマット: numpy.save()/numpy.load()

1.5.2. 特殊関数: `scipy.special`¶

特殊関数は超越関数です。scipy.speciral モジュールの docstring はよく書かれているので全ての関数をここで挙げるということはできません。頻繁に利用されるものは:

Bessel 関数 scipy.special.jn() (整数 n 次の Bessel 関数)

楕円関数 (scipy.special.ellip() Jacobi の楕円関数, ...)

Gamma 関数: scipy.special.gamma() Gamma 関数の log を高精度で与える scipy.special.gammaln() もあります。

Erf、Gaussian の面積: scipy.special.erf()

1.5.3. 線形代数演算: `scipy.linalg`¶

scipy.linalg モジュールは標準的な線形代数演算を提供します、これらは効率的な実装を頼りにしています(BLAS, LAPACK)。

scipy.linalg.det() 関数は正方行列の determinant を計算します:

>>> fromscipyimportlinalg
>>> arr=np.array([[1,2],
... [3,4]])
>>> linalg.det(arr)
-2.0
>>> arr=np.array([[3,2],
... [6,4]])
>>> linalg.det(arr)
0.0
>>> linalg.det(np.ones((3,4)))
Traceback (most recent call last):
...
ValueError: expected square matrix

scipy.linalg.inv() 関数は正方行列の逆行列を計算します:

>>> arr=np.array([[1,2],
... [3,4]])
>>> iarr=linalg.inv(arr)
>>> iarr
array([[-2. ,  1. ],
       [ 1.5, -0.5]])
>>> np.allclose(np.dot(arr,iarr),np.eye(2))
True

最終的な計算結果が特異行列(determinant が 0)の逆行列になった場合は LinAlgError 例外を送出します:

>>> arr=np.array([[3,2],
... [6,4]])
>>> linalg.inv(arr)
Traceback (most recent call last):
...
...LinAlgError: singular matrix

より高度な操作も利用可能です、例: 特異値分解(SVD)
```
>>> arr = np.arange(9).reshape((3, 3)) + np.diag([1, 0, 1])
>>> uarr, spec, vharr = linalg.svd(arr)
```
結果の配列のスペクトルは:
```
>>> spec    
array([ 14.88982544,   0.45294236,   0.29654967])
```
元々の行列は svd の出力を np.dot の行列積によって再構成することができます:
```
>>> sarr = np.diag(spec)
>>> svd_mat = uarr.dot(sarr).dot(vharr)
>>> np.allclose(svd_mat, arr)
True
```
SVD は統計や信号解析によく利用されます。線形システムにおける多くの標準的な分解(QR, LU, Cholesky, Schur) も同様に scipy.linalg で利用可能です。

1.5.4. 高速 Fourier 変換: `scipy.fftpack`¶

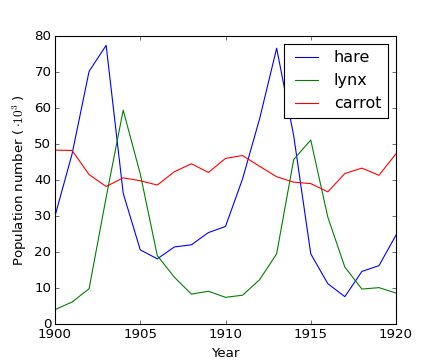
scipy.fftpack モジュールで高速 Fourier 変換を計算するこができます。具体例として、(ノイズを含む)入力信号はこのように表現できます:

>>> time_step=0.02
>>> period=5.
>>> time_vec=np.arange(0,20,time_step)
>>> sig=np.sin(2*np.pi/period*time_vec)+ \
... 0.5*np.random.randn(time_vec.size)

観測者は信号の周波数を知らず、ただ信号 sig のサンプリングした時間ステップだけを知っています。信号は実関数なので Fourier 変換は対称になります。 scipy.fftpack.fftfreq() 関数はサンプル周波数を生成し、 scipy.fftpack.fft() は高速 Fourier 変換を計算します:

>>> fromscipyimportfftpack
>>> sample_freq=fftpack.fftfreq(sig.size,d=time_step)
>>> sig_fft=fftpack.fft(sig)

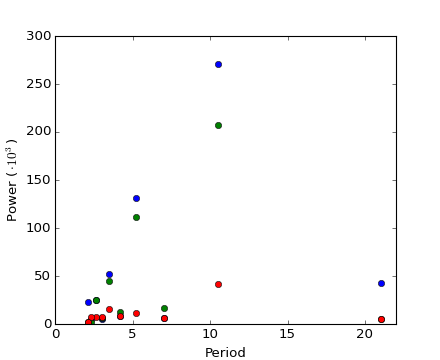
結果のパワースペクトルは対称となるため、スペクトルの正の部分のみで周波数を見つけられます:

>>> pidxs=np.where(sample_freq>0)
>>> freqs=sample_freq[pidxs]
>>> power=np.abs(sig_fft)[pidxs]

[ソースコード, hires.png, pdf]

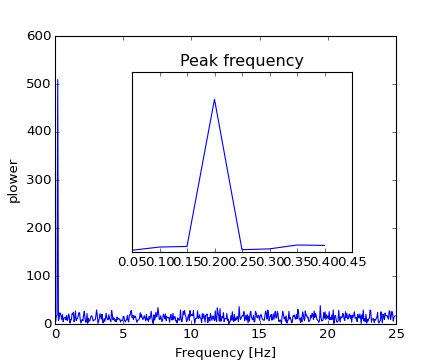
このようにして信号周波数を見つけることができます:

>>> freq=freqs[power.argmax()]
>>> np.allclose(freq,1./period)# check that correct freq is found
True

これで高周波のノイズは Fourier 変換された信号から削除されます:

>>> sig_fft[np.abs(sample_freq)>freq]=0

フィルターされた信号 scipy.fftpack.ifft() 関数を使って計算することができます:

>>> main_sig=fftpack.ifft(sig_fft)

結果は次のようにして見ることができます:

>>> importpylabasplt
>>> plt.figure()
<matplotlib.figure.Figure object at 0x...>
>>> plt.plot(time_vec,sig)
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.plot(time_vec,main_sig,linewidth=3)
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.xlabel('Time [s]')
<matplotlib.text.Text object at 0x...>
>>> plt.ylabel('Amplitude')
<matplotlib.text.Text object at 0x...>

[ソースコード, hires.png, pdf]

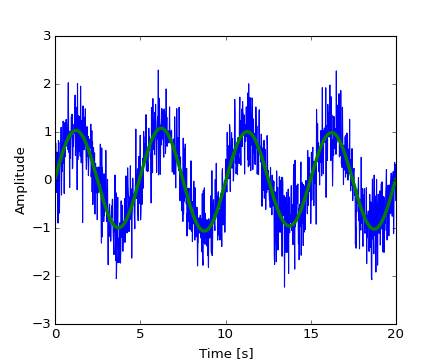
numpy.fft

Numpy にも FFT の実装 (numpy.fft) があります。しかし、大抵の場合は scipy のものの方が、効率的な実装を土台としているので、適しています。

演習例: おおざっぱな周期数探索

[ソースコード, hires.png, pdf]

[ソースコード, hires.png, pdf]

演習例: 画像のガウシアンぼかし

畳み込み:

\[f_1(t) = \int dt'\, K(t-t') f_0(t')\]

\[\tilde{f}_1(\omega) = \tilde{K}(\omega) \tilde{f}_0(\omega)\]

[ソースコード, hires.png, pdf]

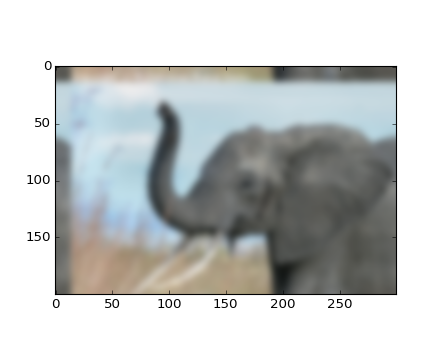
練習問題: 月面着陸画像からのノイズ除去

与えられた画像 moonlanding.png を吟味してみましょう、この画像は周期的なノイズで汚くなっています。この練習問題では、高速 Fourier 変換を利用してノイズを取り除くのを目標とします。
pylab.imread(). を使って画像を読み込みます。
scipy.fftpack から 2次元の FFT 関数を見つけて使いましょう、そして(Fourier 変換した)スペクトルを図にしてみましょう。スペクトルを可視化するときに問題は起きましたか? 起きた場合はどうしてでしょう?
スペクトルは高周波と低周波の要素から成っています。ノイズはスペクトルの高周波部分に含まれています、なのでいくつかの要素を0にしてみましょう(配列のスライスを使いましょう)。
結果の画像を見るために逆 Fourier 変換を適用してみましょう。

1.5.5. 最適化とフィット: `scipy.optimize`¶

最適化問題とは、最小値や等式の数値解を見つける問題のことです。

scipy.optimize モジュールは関数の(スカラーや多次元)関数の極小化や曲線の曲線のフィッティング, そして根の探索ための便利なアルゴリズムを提供しています。:

>>> fromscipyimportoptimize

スカラー関数の極小値を求める

以下の関数を定義してみましょう:

>>> deff(x):
... returnx**2+10*np.sin(x)

そしてプロットしてみましょう:

>>> x=np.arange(-10,10,0.1)
>>> plt.plot(x,f(x))
>>> plt.show()

[ソースコード, hires.png, pdf]

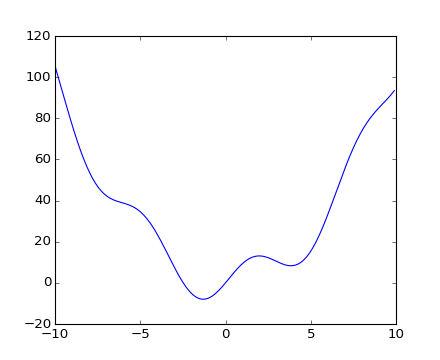
この関数は -1.3 のまわりで大域的な極小値を持ち, 3.8 のまわりで局所的な極小値をもちます。

極小値を見つける一般的で効率的な方法として与えた初期点から勾配が小さくなるように導く方法があります. BFGS アルゴリズムはこの方法に適しています:

>>> optimize.fmin_bfgs(f,0)
Optimization terminated successfully.
         Current function value: -7.945823
         Iterations: 5
         Function evaluations: 24
         Gradient evaluations: 8
array([-1.30644003])

この方法の問題は関数が局所的な極小値を持つ（凸でない）場合, アルゴリズムは初期値に依存して大域的な極小値の代わりに局所的な極小値を見つけるところでしょう:

>>> optimize.fmin_bfgs(f,3,disp=0)
array([ 3.83746663])

初期点に選ぶべき大域的な極小値の近傍を知らない場合, 高い犠牲を払った大域的な最適化に訴えなければいけません. 大域的な極小値を探すために scipy.optimize.basinhopping() を利用します(これはランダムにサンプルした点から局所的オプティマイザを走らせてそれらを組み合わせます):

バージョン 0.12.0 で追加: basinhopping は Scipy のバージョン 0.12.0 で追加されました

>>> optimize.basinhopping(f,0)
                  nfev: 1725
 minimization_failures: 0
                   fun: -7.9458233756152845
                     x: array([-1.30644001])
               message: ['requested number of basinhopping iterations completed successfully']
                  njev: 575
                   nit: 100

他の(少し効率は悪い)グローバルオプティマイザとして scipy.optimize.brute() があります(格子上でブルートフォースに最適化します)。異なるクラスの大域的な最適化問題に対してはより効率的なアルゴリズムがありますが、それらは scipy が扱う範囲から外れます。いくつかの便利な大域的最適化のためのパッケージに OpenOpt_, IPOPT, PyGMO そして PyEvolve があります。

注釈

かつて scipy は anneal ルーチンを持っていましたが、SciPy 0.14.0 で非推奨になり SciPy 0.16.0 で削除されました。

局所的な極小値を探すために値の範囲を scipy.optimize.fminbound(): を使って (0, 10) に制約してみましょう:

>>> xmin_local=optimize.fminbound(f,0,10)
>>> xmin_local
3.8374671...

注釈

関数の極小値を探す方法については、先にある章の数学的最適化: 関数の最小値を求めるでより詳しく議論されています。

スカラー関数の根を求める

根を求める、つまり上の関数 f の f(x)=0 を満す点をみつけるため、例として scipy.optimize.fsolve() を使ってみます:

>>> root=optimize.fsolve(f,1)# our initial guess is 1
>>> root
array([ 0.])

根が1つだけみつかったことに注意して下さい。f の図を調べると -2.5 のまわりに2つめの根があることがわかります。推測に利用する初期値を調整することで厳密な値を得ます:

>>> root2=optimize.fsolve(f,-2.5)
>>> root2
array([-2.47948183])

曲線のフィッティング

f からサンプルしたデータにはノイズがあると仮定します:

>>> xdata=np.linspace(-10,10,num=20)
>>> ydata=f(xdata)+np.random.randn(xdata.size)

サンプルとして与えられたデータの関数系(今の場合 x^2 + sin(x) )がわかっているが、各項の大きさがわからない場合には最小二乗法でフィッティングすることができます。まず、フィットするための関数を定義します:

>>> deff2(x,a,b):
... returna*x**2+b*np.sin(x)

次に a と b を求めるために scipy.optimize.curve_fit() を使います:

>>> guess=[2,2]
>>> params,params_covariance=optimize.curve_fit(f2,xdata,ydata,guess)
>>> params
array([  0.99667386,  10.17808313])

f の極小値と根を求め、フィッティングすることもできました、全ての結果を1つの図に載せてみましょう:

[ソースコード, hires.png, pdf]

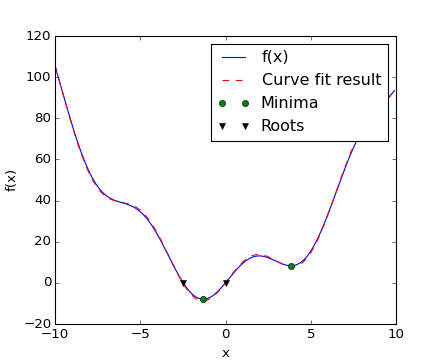
注釈

Scipy >= 0.11 では全ての極小化と求根アルゴリズムの統一されたインターフェース: scipy.optimize.minimize() と scipy.optimize.minimize_scalar() そして scipy.optimize.root() が利用可能です。これらは数多くの異なるアルゴリズムを method キーワードで渡すことができます。

多次元の問題に対しても同じ機能を持ったアルゴリズムを scipy.optimize の中で見つけることができます。

練習問題: 温度データの曲線フィッティング

1月からはじまる各月のアラスカの最大最小温度が与えられています(セルシウスで):
max:  17,  19,  21,  28,  33,  38, 37,  37,  31,  23,  19,  18
min: -62, -59, -56, -46, -32, -18, -9, -13, -25, -46, -52, -58
これらの温度の最大最小をプロットします。

最大温度と最小温度を記述する関数を定義してみましょう。ヒント: この関数は1年の周期を持ちます。ヒント: 時間のオフセットを含みます。

この関数を scipy.optimize.curve_fit() でフィッティングします。

結果をプロットしてみましょう。フィッティングは妥当でしょうか?そうでないならなぜでしょうか?

最大温度と最小温度の時間オフセットはフィッティングの精度を考えて同じといえますか?

練習問題: 2次元最小化

[ソースコード, hires.png, pdf]

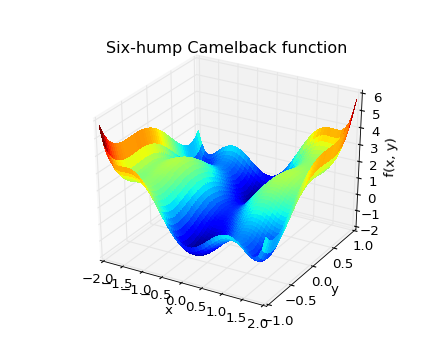
6つこぶラクダの背関数

\[f(x, y) = (4 - 2.1x^2 + \frac{x^4}{3})x^2 + xy + (4y^2 - 4)y^2\]

は大域的、局所的な極小値を複数持っています。この関数の大域的な極小値を求めましょう。

ヒント:

変数は``-2 < x < 2`` と -1 < y < 1 までに制限します。

numpy.meshgrid() と pylab.imshow() 関数を領域を可視化するのに使ってみましょう。

scipy.optimize.fmin_bfgs() や他の多次元の最小化関数を使ってみましょう。

いくつの極小値がありましたか、そしてそれらの点で関数はどんな値をとりましたか? 推測に利用する初期点に (x, y) = (0, 0) を使うと何が起きましたか?

総合演習非線形最小2乗フィット：トポロジカル lidar の点抽出を見てみましょう、他のより高度な例が載っています。

1.5.6. 統計と乱数: `scipy.stats`¶

scipy.stats モジュールは統計分析用のツールや確率過程を確率論的記述を含んでいます。様々な確率過程に対する乱数生成器が numpy.random にあります.

1.5.6.1. 頻度分布と確率密度関数¶

確率過程が観測されると、その頻度分布はその確率仮定の PDF(probability density function 確率密度関数)の推定関数になります:

>>> a=np.random.normal(size=1000)
>>> bins=np.arange(-4,5)
>>> bins
array([-4, -3, -2, -1,  0,  1,  2,  3,  4])
>>> histogram=np.histogram(a,bins=bins,normed=True)[0]
>>> bins=0.5*(bins[1:]+bins[:-1])
>>> bins
array([-3.5, -2.5, -1.5, -0.5,  0.5,  1.5,  2.5,  3.5])
>>> fromscipyimportstats
>>> b=stats.norm.pdf(bins)# norm is a distribution
>>> plt.plot(bins,histogram)
[<matplotlib.lines.Line2D object at ...>]
>>> plt.plot(bins,b)
[<matplotlib.lines.Line2D object at ...>]

[ソースコード, hires.png, pdf]

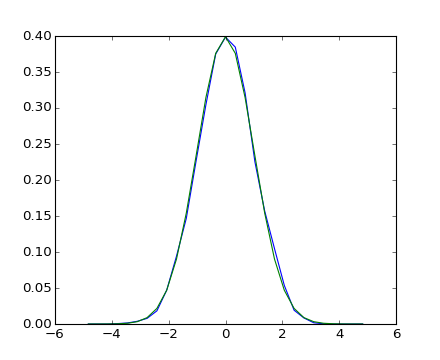
与えられた確率過程が、正規過程のような、どの確率過程の族なのか知ることができれば, 最尤法によって観察量をフィットして分布に内在するパラメータを推定できます. ここで観察したデータを正規過程でフィットします:

>>> loc,std=stats.norm.fit(a)
>>> loc
0.0314345570...
>>> std
0.9778613090...

練習問題: 確率分布

1000 の乱数を形状母数 shape parameter 1のガンマ分布から生成し、頻度分布を例としてプロットします。その確率密度関数を上にプロットできますか(そしてそれは頻度分布と合いますか)?

追加問題: 確率分布は多くの便利なメソッドを持っています。ドキュメンテーション文字列を読んだり、IPython の tab 補完を利用して探ってみましょう。確率変数に対して fit メソッドを利用して形状母数 1 を逆に求めることができますか?

1.5.6.2. 百分位¶

中央値は観測データの上下の中央に位置する値です:

>>> np.median(a)
0.04041769593...

それは百分位点 50 ともいいます, なぜなら観測値の 50% o がその下に位置するからです:

>>> stats.scoreatpercentile(a,50)
0.0404176959...

同様に百分位点 90 も計算できます:

>>> stats.scoreatpercentile(a,90)
1.3185699120...

百分位は累積分布関数の推定関数となります.

1.5.6.3. 統計的検定¶

統計的検定は判断指標です. 例えば Gauss 過程から生成されたと過程される2つの観測の集合があるとき, 2つの集合に有意差があるかを調べるのに T検定 T-test を使うことができます:

>>> a=np.random.normal(0,1,size=100)
>>> b=np.random.normal(1,1,size=10)
>>> stats.ttest_ind(a,b)
(array(-3.177574054...), 0.0019370639...)

ちなみに

検定の結果は以下で構成されます:

T 統計値：2つの確率過程の差に比例し, 有意差の程度を示す数字
p 値: 2つの過程が等価である確率. もし1に近ければ2つの過程はほぼ等価です. 0 に近ければ過程はより異なる意味をもつように思われます.

参考

statistics の章では、統計検定と統計データの読み込みや可視化などの scipy の範囲から外れた手の込んだツールを紹介します。

1.5.7. 補間: `scipy.interpolate`¶

scipy.interpolate は実験データを関数でフィッティングし, 測定していない点を評価するのに便利です. このモジュールは netlib プロジェクトの FITPACK Fortran subroutines を基にしています.

描きだすデータは sin 関数に近い関数にします:

>>> measured_time=np.linspace(0,1,10)
>>> noise=(np.random.random(10)*2-1)*1e-1
>>> measures=np.sin(2*np.pi*measured_time)+noise

scipy.interpolate.interp1d クラスが1次の補間関数を使うために作られています:

>>> fromscipy.interpolateimportinterp1d
>>> linear_interp=interp1d(measured_time,measures)

scipy.interpolate.linear_interp インスタンスに評価したい時間を与える必要があります:

>>> computed_time=np.linspace(0,1,50)
>>> linear_results=linear_interp(computed_time)

kind キーワード引数をオプションとして与えて3次補間を利用することもできます:

>>> cubic_interp=interp1d(measured_time,measures,kind='cubic')
>>> cubic_results=cubic_interp(computed_time)

結果を Matplotlib の figure にまとめます:

[ソースコード, hires.png, pdf]

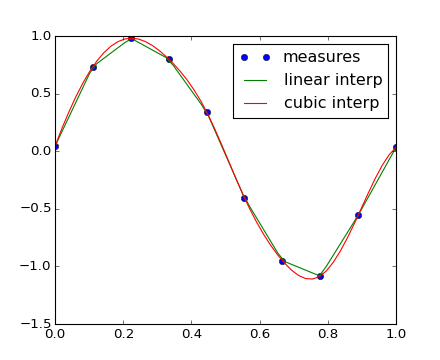
scipy.interpolate.interp2d は scipy.interpolate.interp1d と似ていますが、2次元配列を対象とします。 interp ファミリーについての注意として、関数を評価する時間を測定した時間の範囲内に収める必要があるということです。より高度なスプライン補間の例については Sprogø 気象局の最大風速予測を参照して下さい.

1.5.8. 数値積分: `scipy.integrate`¶

最も一般的な積分ルーチンは scipy.integrate.quad() です:

>>> fromscipy.integrateimportquad
>>> res,err=quad(np.sin,0,np.pi/2)
>>> np.allclose(res,1)
True
>>> np.allclose(err,1-res)
True

他の積分スキームも fixed_quad, quadrature, romberg で利用可能です。

scipy.integrate は常微分方程式 Ordinary Differential Equations (ODE) の積分機能も持っています。特に scipy.integrate.odeint() は LSODA (Livermore Solver for Ordinary Differential equations with Automatic switching for stiff and non-stiff problems) 法を利用した汎用的な integrator です。詳しくは ODEPACK Fortran library を参照して下さい。

odeint は以下の形式の1階の常微分方程式系を解きます:

dy/dt = rhs(y1, y2, .., t0,...)

まずはじめに常微分方程式 dy/dt = -2y を t = 0..4 の区間にわたって y(t=0) = 1 の初期条件のもとで解きます. まずは位置の微分を計算する関数を定義する必要があります:

>>> defcalc_derivative(ypos,time,counter_arr):
... counter_arr+=1
... return-2*ypos
...

追加で与えた引数 counter_arr は単一時間ステップ間で積分が収束するまでに何回実行されたか示すカウンタとして追加されています. カウンタは以下のように定義します:

>>> counter=np.zeros((1,),dtype=np.uint16)

こうして軌道が計算されます:

>>> fromscipy.integrateimportodeint
>>> time_vec=np.linspace(0,4,40)
>>> yvec,info=odeint(calc_derivative,1,time_vec,
... args=(counter,),full_output=True)

微分を与える関数は(時間ステップの回数の)40 回以上呼ばれたことがわかります:

>>> counter
array([129], dtype=uint16)

そして、最初の10回の収束に対しての累積反復回数はこうして得ることができます:

>>> info['nfe'][:10]
array([31, 35, 43, 49, 53, 57, 59, 63, 65, 69], dtype=int32)

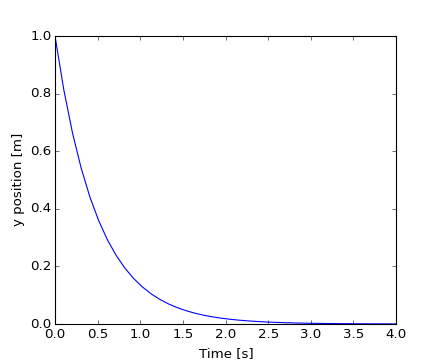
ソルバーは最初の収束により多くの反復回数を必要とします. 軌道として yvec を図にしてみます:

[ソースコード, hires.png, pdf]

Another example with scipy.integrate.odeint() will be a damped spring-mass oscillator (2nd order oscillator). The position of a mass attached to a spring obeys the 2nd order ODE y'' + 2 eps wo y' + wo^2 y = 0 with wo^2 = k/m with k the spring constant, m the mass and eps=c/(2 m wo) with c the damping coefficient. For this example, we choose the parameters as:

>>> mass=0.5# kg
>>> kspring=4# N/m
>>> cviscous=0.4# N s/m

この系は過減衰します、なぜなら:

>>> eps=cviscous/(2*mass*np.sqrt(kspring/mass))
>>> eps<1
True

scipy.integrate.odeint() は二階の方程式をベクトル Y=(y, y') に対する2つの連立一階微分方程式に変換する必要があります。 nu = 2 eps * wo = c / m and om = wo^2 = k/m を定義すると便利です:

>>> nu_coef=cviscous/mass
>>> om_coef=kspring/mass

こうすることで速度と加速度を計算できます:

>>> defcalc_deri(yvec,time,nuc,omc):
... return(yvec[1],-nuc*yvec[1]-omc*yvec[0])
...
>>> time_vec=np.linspace(0,10,100)
>>> yarr=odeint(calc_deri,(1,0),time_vec,args=(nu_coef,om_coef))

最終的な位置と速度の Matplotlib の figure で示します:

[ソースコード, hires.png, pdf]

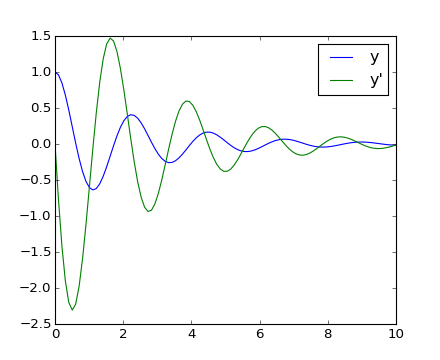
../_images/odeint_damped_spring_mass.png

scipy には偏微分方程式 (PDE) のソルバーは含まれていません. Python の PDE パッケージは, fipy や SfePy などがあります.

1.5.9. 信号解析: `scipy.signal`¶

>>> fromscipyimportsignal

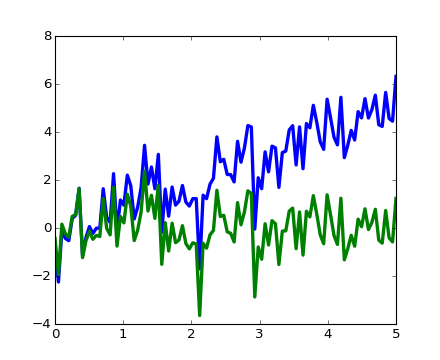
scipy.signal.detrend(): 信号から線形トレンドを除く:

>>> t=np.linspace(0,5,100)
>>> x=t+np.random.normal(size=100)
>>> plt.plot(t,x,linewidth=3)
[<matplotlib.lines.Line2D object at ...>]
>>> plt.plot(t,signal.detrend(x),linewidth=3)
[<matplotlib.lines.Line2D object at ...>]

[ソースコード, hires.png, pdf]

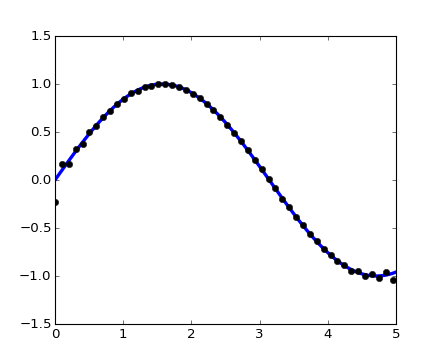
scipy.signal.resample(): FFT を利用して n 点の信号をリサンプルする。:

>>> t=np.linspace(0,5,100)
>>> x=np.sin(t)
>>> plt.plot(t,x,linewidth=3)
[<matplotlib.lines.Line2D object at ...>]
>>> plt.plot(t[::2],signal.resample(x,50),'ko')
[<matplotlib.lines.Line2D object at ...>]

[ソースコード, hires.png, pdf]

scipy.signal は多くの窓関数を持っています: scipy.signal.hamming(), scipy.signal.bartlett(), scipy.signal.blackman()...
scipy.signal はフィルタを持っています has filtering (中央値フィルタ scipy.signal.medfilt(), Wiener scipy.signal.wiener()), しかし, これらについては画像の段落で議論することにします.

1.5.10. 画像処理: `scipy.ndimage`¶

scipy の画像処理向けのサブモジュールは scipy.ndimage です。

>>> fromscipyimportndimage

画像処理ルーチンは実行する処理に応じて分類されています.

1.5.10.1. 画像の幾何学的変換¶

方向, 解像度を変える, ..

>>> fromscipyimportmisc
>>> face=misc.face(gray=True)
>>> shifted_face=ndimage.shift(face,(50,50))
>>> shifted_face2=ndimage.shift(face,(50,50),mode='nearest')
>>> rotated_face=ndimage.rotate(face,30)
>>> cropped_face=face[50:-50,50:-50]
>>> zoomed_face=ndimage.zoom(face,2)
>>> zoomed_face.shape
(1536, 2048)

>>> plt.subplot(151)
<matplotlib.axes._subplots.AxesSubplot object at 0x...>
>>> plt.imshow(shifted_face,cmap=plt.cm.gray)
<matplotlib.image.AxesImage object at 0x...>
>>> plt.axis('off')
(-0.5, 1023.5, 767.5, -0.5)
>>> # etc.

1.5.10.2. 画像フィルタ¶

>>> fromscipyimportmisc
>>> face=misc.face(gray=True)
>>> face=face[:512,-512:]# crop out square on right
>>> importnumpyasnp
>>> noisy_face=np.copy(face).astype(np.float)
>>> noisy_face+=face.std()*0.5*np.random.standard_normal(face.shape)
>>> blurred_face=ndimage.gaussian_filter(noisy_face,sigma=3)
>>> median_face=ndimage.median_filter(noisy_face,size=5)
>>> fromscipyimportsignal
>>> wiener_face=signal.wiener(noisy_face,(5,5))

他にも多くのフィルタが scipy.ndimage.filters や scipy.signal にあり画像に適用することができます。

練習問題

異なるフィルタをかけた画像の頻度分布を比較しなさい.

1.5.10.3. 数理形態学¶

数理形態学 Mathematical morphology は集合論から派生した数学理論です. 幾何構造の特徴付けと変換を行います. 特に2進画像(白と黒のみのモノクロ)はこの理論によって変換でき：変換される集合は近傍に非0値を含みます. また理論はグレースケール画像に対しても拡張されます

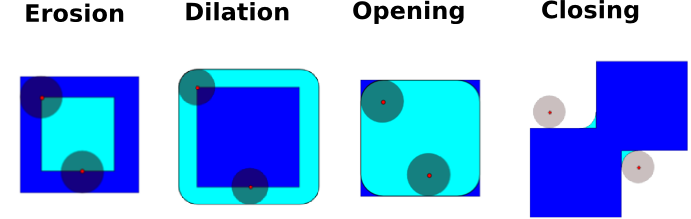
幾何構造を変更するための数理形態学の基本演算は 構造要素 structuring element を使います.

まず構造要素を作ってみましょう:

>>> el=ndimage.generate_binary_structure(2,1)
>>> el
array([[False, True, False],
       [...True, True, True],
       [False, True, False]], dtype=bool)
>>> el.astype(np.int)
array([[0, 1, 0],
       [1, 1, 1],
       [0, 1, 0]])

Erosion

>>> a=np.zeros((7,7),dtype=np.int)
>>> a[1:6,2:5]=1
>>> a
array([[0, 0, 0, 0, 0, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 0, 0, 0, 0, 0]])
>>> ndimage.binary_erosion(a).astype(a.dtype)
array([[0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 1, 0, 0, 0],
       [0, 0, 0, 1, 0, 0, 0],
       [0, 0, 0, 1, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0]])
>>> #Erosion removes objects smaller than the structure
>>> ndimage.binary_erosion(a,structure=np.ones((5,5))).astype(a.dtype)
array([[0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0]])

Dilation

>>> a=np.zeros((5,5))
>>> a[2,2]=1
>>> a
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])
>>> ndimage.binary_dilation(a).astype(a.dtype)
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  1.,  1.,  1.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])

Opening

>>> a=np.zeros((5,5),dtype=np.int)
>>> a[1:4,1:4]=1
>>> a[4,4]=1
>>> a
array([[0, 0, 0, 0, 0],
       [0, 1, 1, 1, 0],
       [0, 1, 1, 1, 0],
       [0, 1, 1, 1, 0],
       [0, 0, 0, 0, 1]])
>>> # Opening removes small objects
>>> ndimage.binary_opening(a,structure=np.ones((3,3))).astype(np.int)
array([[0, 0, 0, 0, 0],
       [0, 1, 1, 1, 0],
       [0, 1, 1, 1, 0],
       [0, 1, 1, 1, 0],
       [0, 0, 0, 0, 0]])
>>> # Opening can also smooth corners
>>> ndimage.binary_opening(a).astype(np.int)
array([[0, 0, 0, 0, 0],
       [0, 0, 1, 0, 0],
       [0, 1, 1, 1, 0],
       [0, 0, 1, 0, 0],
       [0, 0, 0, 0, 0]])

Closing: ndimage.binary_closing

練習問題

opening が eroding 後に dilating することを確かめなさい.

opening 操作は小さい構造を取り除き, closing 操作は小さな穴を埋めます. これらの操作は画像の「ごみとり」に使えます.

>>> a=np.zeros((50,50))
>>> a[10:-10,10:-10]=1
>>> a+=0.25*np.random.standard_normal(a.shape)
>>> mask=a>=0.5
>>> opened_mask=ndimage.binary_opening(mask)
>>> closed_mask=ndimage.binary_closing(opened_mask)

練習問題

再構成された正方形が元の領域より小さいことを確かめましょう (opening の前に closing を行うと逆のことが起こるはずです).

gray-valued 画像については, erodingは (dilation は)注目するピクセルを中心とする構造要素内のピクセルの最小値に(最大値に)置き換えます:

>>> a=np.zeros((7,7),dtype=np.int)
>>> a[1:6,1:6]=3
>>> a[4,4]=2;a[2,3]=1
>>> a
array([[0, 0, 0, 0, 0, 0, 0],
       [0, 3, 3, 3, 3, 3, 0],
       [0, 3, 3, 1, 3, 3, 0],
       [0, 3, 3, 3, 3, 3, 0],
       [0, 3, 3, 3, 2, 3, 0],
       [0, 3, 3, 3, 3, 3, 0],
       [0, 0, 0, 0, 0, 0, 0]])
>>> ndimage.grey_erosion(a,size=(3,3))
array([[0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 0, 0],
       [0, 0, 3, 2, 2, 0, 0],
       [0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0]])

1.5.10.4. 画像の測定¶

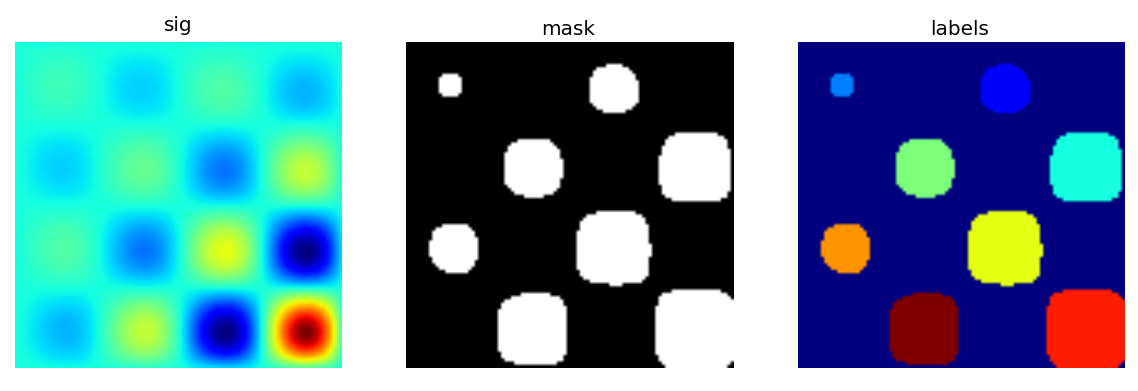
まず素敵な人工的2進画像を作りましょう.

>>> x,y=np.indices((100,100))
>>> sig=np.sin(2*np.pi*x/50.)*np.sin(2*np.pi*y/50.)*(1+x*y/50.**2)**2
>>> mask=sig>1

画像内のオブジェクトの色々な情報を見ることができます:

>>> labels,nb=ndimage.label(mask)
>>> nb
8
>>> areas=ndimage.sum(mask,labels,range(1,labels.max()+1))
>>> areas
array([ 190.,   45.,  424.,  278.,  459.,  190.,  549.,  424.])
>>> maxima=ndimage.maximum(sig,labels,range(1,labels.max()+1))
>>> maxima
array([  1.80238238,   1.13527605,   5.51954079,   2.49611818,
         6.71673619,   1.80238238,  16.76547217,   5.51954079])
>>> ndimage.find_objects(labels==4)
[(slice(30L, 48L, None), slice(30L, 48L, None))]
>>> sl=ndimage.find_objects(labels==4)
>>> importpylabaspl
>>> pl.imshow(sig[sl[0]])
<matplotlib.image.AxesImage object at ...>

より高度な例は総合演習 Image processing application: counting bubbles and unmolten grains を参照して下さい。

1.5.11. 科学技術計算の総合演習 ¶

総合演習では Numpy, Scipy そして Matplotlib を主に使います. Python での科学技術計算を実生活における例として使うことを最初の目的としています. 1度土台を築けば, 興味あるユーザはさらなる演習を試みていくことでしょう.

Exercises:

Proposed solutions:

1.5.11.4. 画像処理練習問題解答例: ガラスの中の非融解粒