1.5.11.2. 非線形最小2乗フィット：トポロジカル lidar の点抽出

この演習問題の目的は特定のデータに対してモデルをフィットすることです. このチュートリアルでは lidar のデータを使います. lidar のデータについては以下の導入の段落で説明します. もし待ち切れなくてすぐにでも実践したければ飛して直接 読み込みと可視化 に向かって下さい.

1.5.11.2.1. 導入

Lidar は光学距離計測系で, 距離測定のために散乱光の性質を解析します. 多くの lidar は短いインパルス光を対象に対して放出し反射信号を記録します. 信号は解析されて lidar と対象の間の距離が抽出されます.

トポロジカル lidar はそのような計測系を飛行機の機体に搭載したものです. 地球と飛行機間の距離を即停止, 地球の地形の情報を伝えます(詳しくは [1] を見てください).

[1]Mallet, C. and Bretar, F. Full-Waveform Topographic Lidar: State-of-the-Art. ISPRS Journal of Photogrammetry and Remote Sensing 64(1), pp.1-16, January 2009 http://dx.doi.org/10.1016/j.isprsjprs.2008.09.007

チュートリアルでの目的は Lidar 系に記録された波形 [2] を解析することです. この信号は中心にピークを持ち, 振幅から距離やいくつかの特徴を計算できます. レーザービームの足跡が地球上約 1m に及ぶと, 2方向伝搬の間でビームは複数の対象に当ることがあります. (例えば木やビルの頂上と地面)レーザービームが各対象に当ることでその寄与の和は複数のピークを持った複雑な信号を作りだします, 各ピークに1つの対象の情報が含まれています.

これらのデータから情報を取り出す最新技術の1つはデータをレーザービームに当った寄与を表現する Gauss 関数の和として分解する方法があります.

したがって, 波形を1つの Gauss 関数または Gauss 関数の和でフィットするために sicpy.optimize モジュールを使います.

1.5.11.2.2. 読み込みと可視化

最初の波形を読み込みます:

>>> import numpy as np

>>> waveform_1 = np.load('data/waveform_1.npy')

そして可視化します:

>>> import matplotlib.pyplot as plt

>>> t = np.arange(len(waveform_1))

>>> plt.plot(t, waveform_1) 

[<matplotlib.lines.Line2D object at ...>]

>>> plt.show()
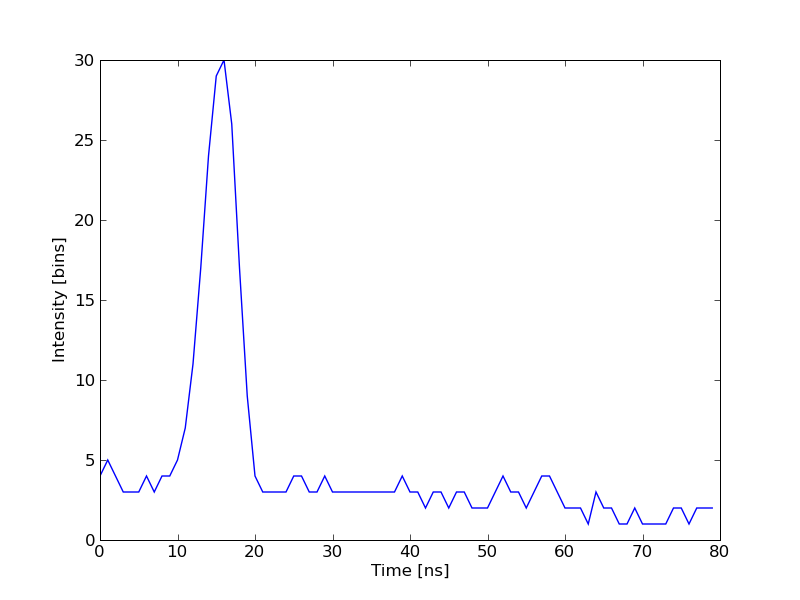
../../_images/waveform_1.png

気づくと思いますが, この波形は1つのピークを持った 80 の区画に分けられた信号です.

1.5.11.2.3. 波形を単純な Gauss モデルでフィット

信号は単純なので1つの Gauss 関数とバックグラウンドノイズに対応するずれとして表現できます. 信号を関数でフィットするためには以下をしなければいけません:

  • モデルを定義

  • 初期解を提案

  • scipy.optimize.leastsq を呼びだす

1.5.11.2.3.1. モデル

Gauss 関数を定義します

\[B + A \exp\left\{-\left(\frac{t-\mu}{\sigma}\right)^2\right\}\]

Python では以下で定義できます:

>>> def model(t, coeffs):

...    return coeffs[0] + coeffs[1] * np.exp( - ((t-coeffs[2])/coeffs[3])**2 )

ここで

  • coeffs[0] は \(B\) (ノイズ)

  • coeffs[1] は \(A\) (振幅)

  • coeffs[2] は \(\mu\) (中心)

  • coeffs[3] は \(\sigma\) (幅)

1.5.11.2.3.2. 初期解

グラフを見て初期の近似解を例えば以下のようにしてみます:

>>> x0 = np.array([3, 30, 15, 1], dtype=float)

1.5.11.2.3.3. フィット

scipy.optimize.leastsq は引数として与えた関数の2乗の和を最小化します. 基本的に最小化する関数は残余(データとモデルの差)です:

>>> def residuals(coeffs, y, t):

...     return y - model(t, coeffs)

さて以下の引数で sipy.optimize.leastsq() を呼び出して解を得ましょう:

  • 最小化する関数

  • 初期解

  • 関数に渡す追加の引数

>>> from scipy.optimize import leastsq

>>> x, flag = leastsq(residuals, x0, args=(waveform_1, t))

>>> print(x)

[  2.70363341  27.82020742  15.47924562   3.05636228]

そして解を可視化します:

>>> plt.plot(t, waveform_1, t, model(t, x)) 

[<matplotlib.lines.Line2D object at ...>, <matplotlib.lines.Line2D object at ...>]

>>> plt.legend(['waveform', 'model']) 

<matplotlib.legend.Legend object at ...>

>>> plt.show()

注目： scipy v0.8 以上では scipy.optimize.curve_fit() を使うべきです. これはモデルとデータを引数としてとるので残差を定義する必要はありません.

1.5.11.2.4. より進んで

  • より複雑な波形に挑戦してみましょう(例として data/waveform_2.npy)これは3つの著しいピークを含みます. 1つの Gauss 関数 の代わりに3つの Gauss 関数の和を使う必要があります.

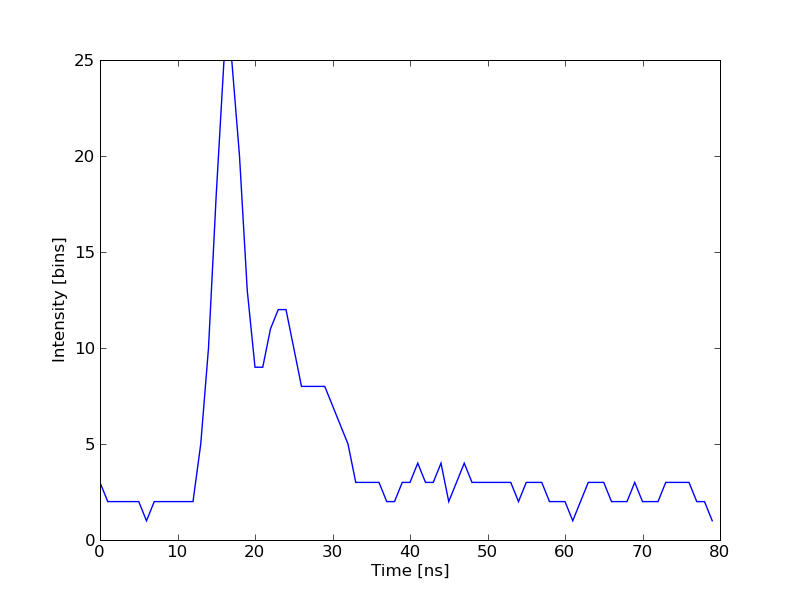
../../_images/waveform_2.png

  • leastsq を数値的に評価するよりも関数行列式を計算する関数を明示的に書いた方が場合があります. 残余の関数行列式を計算する関数を作り, leastsq の入力に使ってみましょう.

  • 信号の小さなピークを検出したい, または初期解が妥当でない場合には与えたアルゴリズムは不満足な結果を与えます. パラメータの拘束条件を追加することでこの制限に打ち克つことができます. 追加できる アプリオリ な知識の例は変数の符号です(これらは全て正).

    以下の初期解:

    >>> x0 = np.array([3, 50, 20, 1], dtype=float)

    を使って scipy.optimize.leastsq() と拘束条件を追加して scipy.optimize.fmin_slsqp() で得た結果を比較してみましょう.

[2]

このチュートリアルで使った実演データは FullAnalyze software から入手できます, これらは GIS DRAIX が快く提供してくれました.