3.1. Python での統計¶
著者: Gaël Varoquaux
必要なもの
標準的な Python の科学技術環境 (numpy, scipy, matplotlib)
- Pandas
- Statsmodels
- Seaborn
Python と依存ライブラリをインストールするのにに Anaconda Python か Enthought Canopy をダウンロードするか、Ubuntu や他の Linux ならパッケージマネージャーを利用する、ことをおすすめします。
参考
Python での Bayesian 統計
この章では Bayesian 統計については扱いません。Bayesian モデリングに関して特化したものとしては PyMC があり、 Python での確率を扱うプログラムを実装しています。
ちなみに
どうして統計に Python を使うのか?
R は統計に特化した言語です。Python は汎用の言語で、統計モジュールを持っています。R は Python に比べて多くの統計解析の機能と特化した構文を持っています。しかし、つ画像解析、テキストマイニング、物理的な実験の制御、といった複雑な解析のパイプライン、を構築したりする場合は Python の幅広い機能が大きな価値となります。
目次
ちなみに
このドキュメントでは Python の入力は “>>>” で表されます。
免責事項: 性別に関する質問
このチュートリアルでのいくつかの例は性別に関する問題が選ばれています。その理由は、これらの質問は主張の真偽の扱いが実際に多くの人にとって重要な問題だからです。
3.1.1. データの表示と対話操作¶
3.1.1.1. 表データ¶
複数の 測定 または 標本 が異なる 属性 や 特徴 の組みで表わされるものとします。データば2次元の表または行列と考えることができ、列がデータの異なる属性で表が測定を表します。例えば examples/brain_size.csv に含まれるデータ:
"";"Gender";"FSIQ";"VIQ";"PIQ";"Weight";"Height";"MRI_Count"
"1";"Female";133;132;124;"118";"64.5";816932
"2";"Male";140;150;124;".";"72.5";1001121
"3";"Male";139;123;150;"143";"73.3";1038437
"4";"Male";133;129;128;"172";"68.8";965353
"5";"Female";137;132;134;"147";"65.0";951545
3.1.1.2. panda データフレーム¶
ちなみに
pandas モジュールの pandas.DataFrame にデータを記録し、操作しましょう。これは Python でのスプレッドシート代わりに使えます。これは 2次元の numpy 配列と違って名前つきの行を持ち、行に異なるデータ型を混在させることができ、凝った要素選択やピボット機能を持ちます。
3.1.1.2.1. データフレームの作成: データファイルの読み込みや配列の変換¶
CSV ファイルからの読み込み: (Willerman et al. 1991 による) 脳のサイズと重さと IQ の測定値を与えた上記のファイルを利用します、このデータは数値とカテゴリ変数が混ざっています:
>>> import pandas
>>> data = pandas.read_csv('examples/brain_size.csv', sep=';', na_values=".")
>>> data
Unnamed: 0 Gender FSIQ VIQ PIQ Weight Height MRI_Count
0 1 Female 133 132 124 118 64.5 816932
1 2 Male 140 150 124 NaN 72.5 1001121
2 3 Male 139 123 150 143 73.3 1038437
3 4 Male 133 129 128 172 68.8 965353
4 5 Female 137 132 134 147 65.0 951545
...
警告
欠損値
2番目に重要なこととして CSV ファイルには欠損値があります。欠損値 (NA = 該当なし) マーカーを指定しない場合、その値を統計解析できません。
配列からの作成: pandas.DataFrame`は1次元の「系列」の辞書とみなすこともできます、例えばリストの配列など。以下のように3つの ``numpy` 配列があれば:
>>> import numpy as np
>>> t = np.linspace(-6, 6, 20)
>>> sin_t = np.sin(t)
>>> cos_t = np.cos(t)
これらを pandas.DataFrame としてみましょう:
>>> pandas.DataFrame({'t': t, 'sin': sin_t, 'cos': cos_t})
cos sin t
0 0.960170 0.279415 -6.000000
1 0.609977 0.792419 -5.368421
2 0.024451 0.999701 -4.736842
3 -0.570509 0.821291 -4.105263
4 -0.945363 0.326021 -3.473684
5 -0.955488 -0.295030 -2.842105
6 -0.596979 -0.802257 -2.210526
7 -0.008151 -0.999967 -1.578947
8 0.583822 -0.811882 -0.947368
...
他の入力形式: pandas は SQL やエクセルファイルやその他の形式からの入力データを扱えます。 pandas documentation を参照して下さい。
3.1.1.2.2. データの操作¶
data は a pandas.DataFrame で R のデータフレームを似せたものです:
>>> data.shape # 40 rows and 8 columns
(40, 8)
>>> data.columns # It has columns
Index([u'Unnamed: 0', u'Gender', u'FSIQ', u'VIQ', u'PIQ', u'Weight', u'Height', u'MRI_Count'], dtype='object')
>>> print(data['Gender']) # Columns can be addressed by name
0 Female
1 Male
2 Male
3 Male
4 Female
...
>>> # Simpler selector
>>> data[data['Gender'] == 'Female']['VIQ'].mean()
109.45
注釈
大きなデータフレームを手っ取り早く見るには describe メソッドを利用します: pandas.DataFrame.describe().
groupby: データフレームをカテゴリ変数に従って分割します:
>>> groupby_gender = data.groupby('Gender')
>>> for gender, value in groupby_gender['VIQ']:
... print((gender, value.mean()))
('Female', 109.45)
('Male', 115.25)
groupby_gender は強力なオブジェクトで、データフレームをグループ分けしたものに対する多くの演算結果を示してくれます。
>>> groupby_gender.mean()
Unnamed: 0 FSIQ VIQ PIQ Weight Height MRI_Count
Gender
Female 19.65 111.9 109.45 110.45 137.200000 65.765000 862654.6
Male 21.35 115.0 115.25 111.60 166.444444 71.431579 954855.4
ちなみに
groupby_gender に対して tab 補完することでより多くのことがわかります。他のグループ化関数として median, count (様々な部分集合内での欠損値の量を確認するのに便利) あるいは sum があります。グループ化は遅延評価されるので、集約関数が適用されるまで何も実行されません。
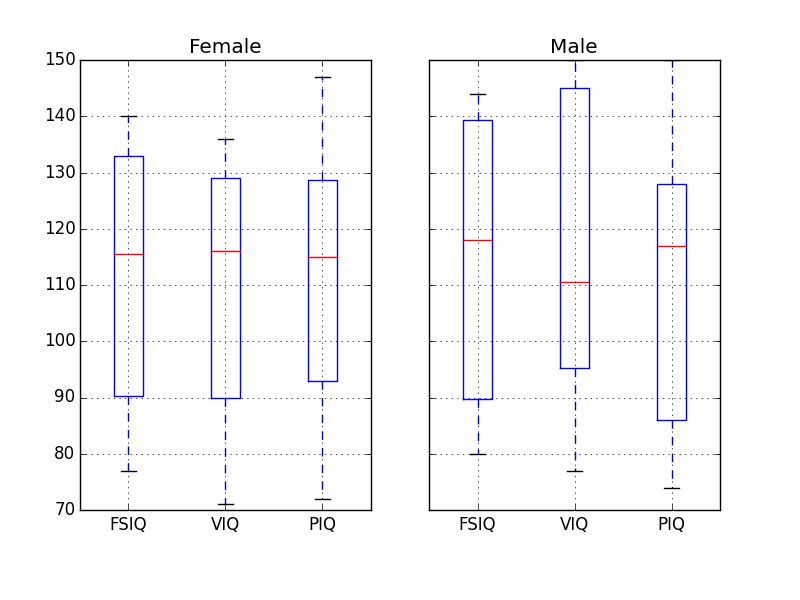
練習問題
全母集団に対する VIQ の平均はいくつですか?
この調査何人の男女が含まれていますか?
ヒント 「tab 補完」を利用して、上の例での ‘mean’ の代わりに呼び出せるメソッドを調べてみましょう。
MRI count の平均を対数単位で表わすといくつになりますか、男女で比較するとどうですか?
注釈
groupby_gender.boxplot が上の図で利用されています (この例 を見てください)。
3.1.1.2.3. データのプロット¶
Pandas はいくつかのプロットツールを含んでおり (pandas.tools.plotting これは裏で matplotlib を利用します) データフレーム内のデータの統計値を表示します:
散布図行列:
>>> from pandas.tools import plotting
>>> plotting.scatter_matrix(data[['Weight', 'Height', 'MRI_Count']])
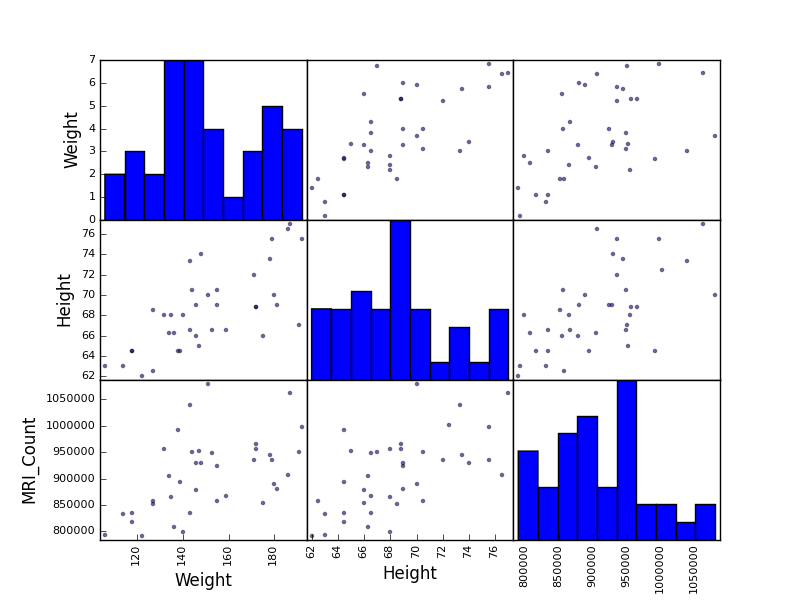
>>> plotting.scatter_matrix(data[['PIQ', 'VIQ', 'FSIQ']])
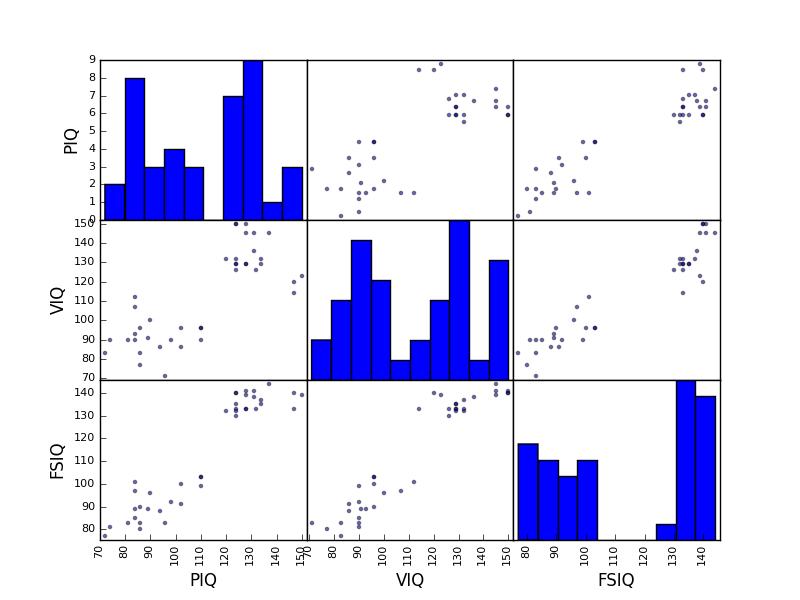
練習問題
男性のみ、女性のみで散布図行列をプロットしてみましょう。2つの部分母集団は性別に対応すると思いますか?
3.1.2. 仮説検定: 2つのグループの比較¶
単純な statistical tests には scipy のサブモジュール scipy.stats が利用できます:
>>> from scipy import stats
参考
Scipy は広範なライブラリです。手っ取り早くライブラリ全体の概要をつかむには scipy の章を見ましょう。
3.1.2.1. Student の t 検定: 最も単純な統計検定¶
3.1.2.1.1. 1標本t検定: 母集団平均の値を検定¶
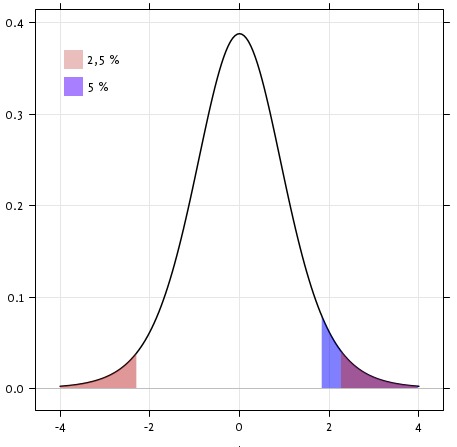
scipy.stats.ttest_1samp() はデータの母集団平均が与えられた値と等しい見込みがあるかを検定します(厳密にいえば、観測値が与えられた母集団平均を持つ Gauss 分布に従うか)。この関数は T statistic, と p-value を返します(関数の help をみてください):
>>> stats.ttest_1samp(data['VIQ'], 0)
(...30.088099970..., 1.32891964...e-28)
ちなみに
p値が 10^-28 なので IQ (VIQ 測定値) の母集団平均は 0 ではないと主張できます。
3.1.2.1.2. 2標本t検定: 母集団間の差異を検定¶
上で男性、女性の母集団で VIQ の平均の値が違うことを確認しました。これが有意な違いなのか確認するため scipy.stats.ttest_ind() で2つの母集団に対して t検定します:
>>> female_viq = data[data['Gender'] == 'Female']['VIQ']
>>> male_viq = data[data['Gender'] == 'Male']['VIQ']
>>> stats.ttest_ind(female_viq, male_viq)
(...-0.77261617232..., 0.4445287677858...)
3.1.2.2. 対応のある検定: 同じ個体に繰り返し測定¶
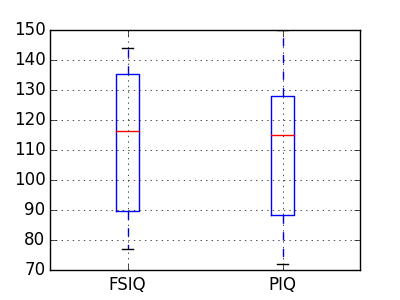
PIQ, VIQ そして FSIQ は3つの IQ の指標を与えます。FISQ と PIQ が有意に異なるかを検定しましょう。2つの標本検定が利用できます:
>>> stats.ttest_ind(data['FSIQ'], data['PIQ'])
(...0.46563759638..., 0.64277250...)
この方法の問題点は、観測値の間の関連を無視していることです: FSIQ と PIQ は同じに対して測定されています。そのため被験者間の変動によって分散が交絡します、そしてそれは “対応のある検定”, または “repeated measures test” で取り除くことができます:
>>> stats.ttest_rel(data['FSIQ'], data['PIQ'])
(...1.784201940..., 0.082172638183...)
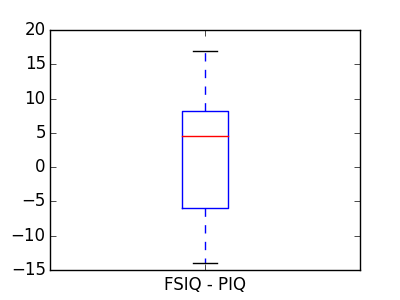
これは差分に対する1標本検定と等価です:
>>> stats.ttest_1samp(data['FSIQ'] - data['PIQ'], 0)
(...1.784201940..., 0.082172638...)
t検定は誤差が Gauss 分布に従うと仮定します。その仮定を緩めるのに Wilcoxon signed-rank test を利用することができます:
>>> stats.wilcoxon(data['FSIQ'], data['PIQ'])
(274.5, 0.106594927...)
注釈
対応のない検定としては scipy.stats.mannwhitneyu() で Mann–Whitney U test が該当します。
練習問題
男性と女性の重さの差を検定しましょう。
ノンパラメトリック検定で男性と女性の間の VIQ の差を検定しましょう。
結論: データは男性と女性で VIQ が異なるという仮説を支持しないことがわかりました。
3.1.3. 線形モデル、多変数、そして分散分析¶
3.1.3.1. Python で “formulas” を利用して統計モデルを指定する¶
3.1.3.1.1. 単純な線形回帰¶
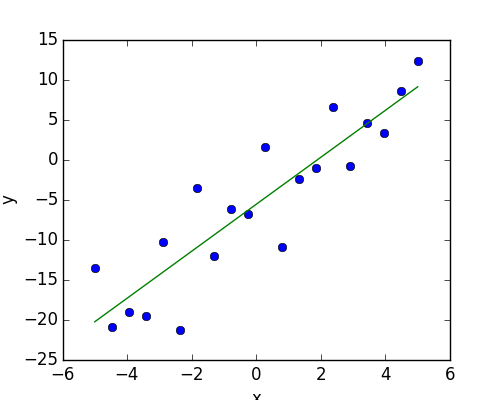
二組みの観測値 x と y が与えられ y が x の線形な関数だという仮定を検定したいとします。いいかえると:
\(y = x * coef + intercept + e\)
ここで e は測定値のノイズです。ここで statmodels <http://statsmodels.sourceforge.net/> モジュールを利用します:
線形モデルにフィットします。戦略として最も単純な ordinary least squares (OLS) を利用します。
coef がゼロでないことを検定します。
まず、モデルに従うシミュレーションデータを生成します:
>>> import numpy as np
>>> x = np.linspace(-5, 5, 20)
>>> np.random.seed(1)
>>> # normal distributed noise
>>> y = -5 + 3*x + 4 * np.random.normal(size=x.shape)
>>> # Create a data frame containing all the relevant variables
>>> data = pandas.DataFrame({'x': x, 'y': y})
次に OLS モデルを指定してフィットさせます:
>>> from statsmodels.formula.api import ols
>>> model = ols("y ~ x", data).fit()
フィットした結果から様々な統計量を除くことができます:
>>> print(model.summary())
OLS Regression Results
==========================...
Dep. Variable: y R-squared: 0.804
Model: OLS Adj. R-squared: 0.794
Method: Least Squares F-statistic: 74.03
Date: ... Prob (F-statistic): 8.56e-08
Time: ... Log-Likelihood: -57.988
No. Observations: 20 AIC: 120.0
Df Residuals: 18 BIC: 122.0
Df Model: 1
==========================...
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------...
Intercept -5.5335 1.036 -5.342 0.000 -7.710 -3.357
x 2.9369 0.341 8.604 0.000 2.220 3.654
==========================...
Omnibus: 0.100 Durbin-Watson: 2.956
Prob(Omnibus): 0.951 Jarque-Bera (JB): 0.322
Skew: -0.058 Prob(JB): 0.851
Kurtosis: 2.390 Cond. No. 3.03
==========================...
専門用語:
statsmodel は統計用語を使います: statsmodel の y 変数は ‘endogenous’ と呼ばれます、一方で x 変数は exogenous と呼ばれます。詳しくは ここ に議論があります。
単純化のために y (endogenous) が予測したい値であるとし、 x (exogenous) が予測のための特徴を表わす量だとします。
練習問題
上記モデルのパラメータ推定します: ヒント: tab 補完して、関連する属性を探しましょう。
3.1.3.1.2. カテゴリ変数: グループや複数のカテゴリ間で比較¶
脳のサイズデータに立ち戻ってみましょう:
>>> data = pandas.read_csv('examples/brain_size.csv', sep=';', na_values=".")
男性と女性の IQ を線形モデルで比較することができます:
>>> model = ols("VIQ ~ Gender + 1", data).fit()
>>> print(model.summary())
OLS Regression Results
==========================...
Dep. Variable: VIQ R-squared: 0.015
Model: OLS Adj. R-squared: -0.010
Method: Least Squares F-statistic: 0.5969
Date: ... Prob (F-statistic): 0.445
Time: ... Log-Likelihood: -182.42
No. Observations: 40 AIC: 368.8
Df Residuals: 38 BIC: 372.2
Df Model: 1
==========================...
coef std err t P>|t| [95.0% Conf. Int.]
-----------------------------------------------------------------------...
Intercept 109.4500 5.308 20.619 0.000 98.704 120.196
Gender[T.Male] 5.8000 7.507 0.773 0.445 -9.397 20.997
==========================...
Omnibus: 26.188 Durbin-Watson: 1.709
Prob(Omnibus): 0.000 Jarque-Bera (JB): 3.703
Skew: 0.010 Prob(JB): 0.157
Kurtosis: 1.510 Cond. No. 2.62
==========================...
モデルを指定するための Tips
カテゴリ変数の強制:’Gender’ は自動的にカテゴリ変数と判定され、異なる値はそれぞれ異なるものとして扱われます。
整数のカラムはカテゴリ変数として扱うように強制できます:
>>> model = ols('VIQ ~ C(Gender)', data).fit()
Intercept: formula に - 1 を使うことで intercept を除くことができます、また + 1 を使うことで intercept を使うように強制できます。
ちなみに
デフォルトでは statsmodel はカテゴリ変数を K のとりうる値を持ち K-1 の「ダミー」変数として(最後レベルが intercept 項に吸収されます)扱います。これはほとんどの場合デフォルトの選択としてよく動きます ー 一方で、カテゴリ変数に異なるエンコーディングを変数することもできます (http://statsmodels.sourceforge.net/devel/contrasts.html)。
FSIQ と PIQ の違いに関する t検定との関連
異なる IQ の種類を比較するために “long-form” の表を作成して、IQ の一覧を作成します、ここで IQ の種類はカテゴリ変数としてあつかわれます:
>>> data_fisq = pandas.DataFrame({'iq': data['FSIQ'], 'type': 'fsiq'})
>>> data_piq = pandas.DataFrame({'iq': data['PIQ'], 'type': 'piq'})
>>> data_long = pandas.concat((data_fisq, data_piq))
>>> print(data_long)
iq type
0 133 fsiq
1 140 fsiq
2 139 fsiq
...
31 137 piq
32 110 piq
33 86 piq
...
>>> model = ols("iq ~ type", data_long).fit()
>>> print(model.summary())
OLS Regression Results
...
==========================...
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------...
Intercept 113.4500 3.683 30.807 0.000 106.119 120.781
type[T.piq] -2.4250 5.208 -0.466 0.643 -12.793 7.943
...
前のt検定での IQ の種類の影響に関するt検定と対応する p値にと同じ値を取得できることが確認できます:
>>> stats.ttest_ind(data['FSIQ'], data['PIQ'])
(...0.46563759638..., 0.64277250...)
3.1.3.2. 多変数回帰: 複数の要因を含む場合¶
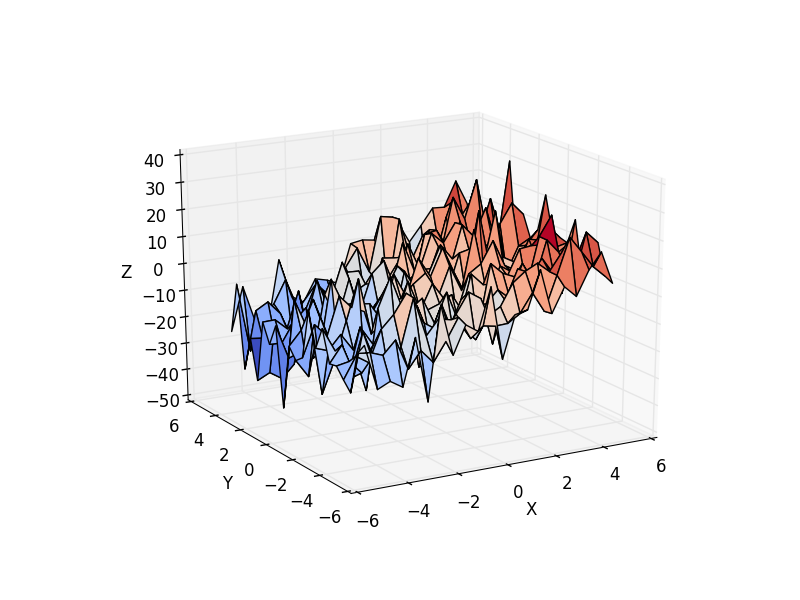
(独立変数) z を2つの変数 x と y で説明する線形モデルを考えます。
\(z = x \, c_1 + y \, c_2 + i + e\)
このモデルは3次元で (x, y, z) の点群を平面でフィットする問題とみなすことができます。
例: アヤメのデータ (examples/iris.csv)
ちなみに
sepal と petal のサイズは関連する傾向にあります: 大きい花は大きい! しかし、さらに種の分類による影響がありそうです。
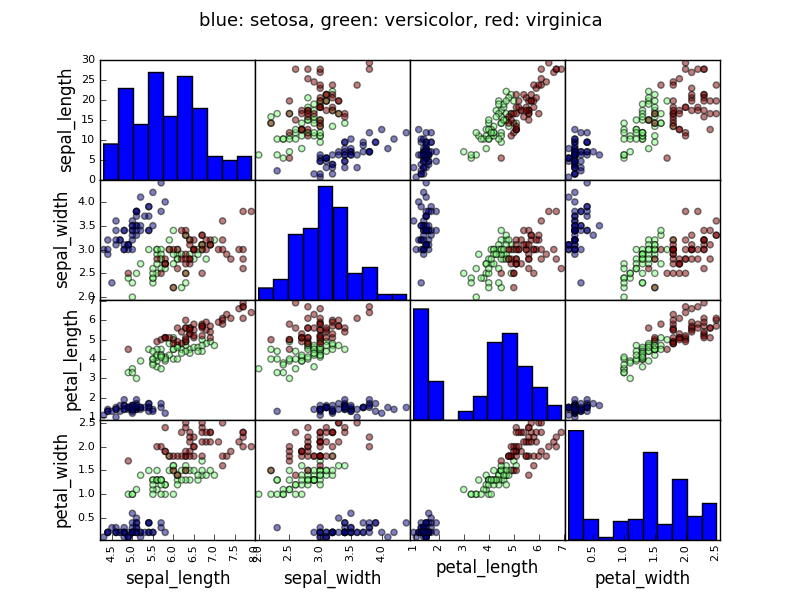
>>> data = pandas.read_csv('examples/iris.csv')
>>> model = ols('sepal_width ~ name + petal_length', data).fit()
>>> print(model.summary())
OLS Regression Results
==========================...
Dep. Variable: sepal_width R-squared: 0.478
Model: OLS Adj. R-squared: 0.468
Method: Least Squares F-statistic: 44.63
Date: ... Prob (F-statistic): 1.58e-20
Time: ... Log-Likelihood: -38.185
No. Observations: 150 AIC: 84.37
Df Residuals: 146 BIC: 96.41
Df Model: 3
==========================...
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------...
Intercept 2.9813 0.099 29.989 0.000 2.785 3.178
name[T.versicolor] -1.4821 0.181 -8.190 0.000 -1.840 -1.124
name[T.virginica] -1.6635 0.256 -6.502 0.000 -2.169 -1.158
petal_length 0.2983 0.061 4.920 0.000 0.178 0.418
==========================...
Omnibus: 2.868 Durbin-Watson: 1.753
Prob(Omnibus): 0.238 Jarque-Bera (JB): 2.885
Skew: -0.082 Prob(JB): 0.236
Kurtosis: 3.659 Cond. No. 54.0
==========================...
3.1.3.3. 事後仮説検定: analysis of variance (ANOVA)¶
上のアヤメの例では、sepal の幅の影響を除いて petal の長さが versicolor と virginica で異なるという仮説を検定しようとしました。これは上で推定した線形モデルでの versicolor と virginica に関連づけられた係数の間の差を検定することでできます(これが分散分析, ANOVA です)。このために ‘contrast’ のベクトル を推定したパラメーターから作ります: "name[T.versicolor] - name[T.virginica]" を F-test で検定します:
>>> print(model.f_test([0, 1, -1, 0]))
<F test: F=array([[ 3.24533535]]), p=[[ 0.07369059]], df_denom=146, df_num=1>
差は有意でしょうか?
練習問題
脳のサイズと IQ のデータに戻って、脳のサイズ、高さ、重さの影響を除いて、男性と女性の VIQ の間に差があるか検定しましょう。
3.1.4. より多くの可視化: 統計調査のための seaborn¶
Seaborn は pandas データフレームを単純な統計フィットと組み合わせてプロットします。
500人の賃金とその他の個人情報を含むデータを考えます (Berndt, ER. The Practice of Econometrics. 1991. NY: Addison-Wesley)。
ちなみに
賃金データを読み込んでプロットするコードの完全版が corresponding example にあります。
>>> print data
EDUCATION SOUTH SEX EXPERIENCE UNION WAGE AGE RACE \
0 8 0 1 21 0 0.707570 35 2
1 9 0 1 42 0 0.694605 57 3
2 12 0 0 1 0 0.824126 19 3
3 12 0 0 4 0 0.602060 22 3
...
3.1.4.1. Pairplot: 散布図行列¶
seaborn.pairplot() を利用して散布図行列を表示することで、連続変数の間の関連に対する直感が容易に得られます:
>>> import seaborn
>>> seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'],
... kind='reg')
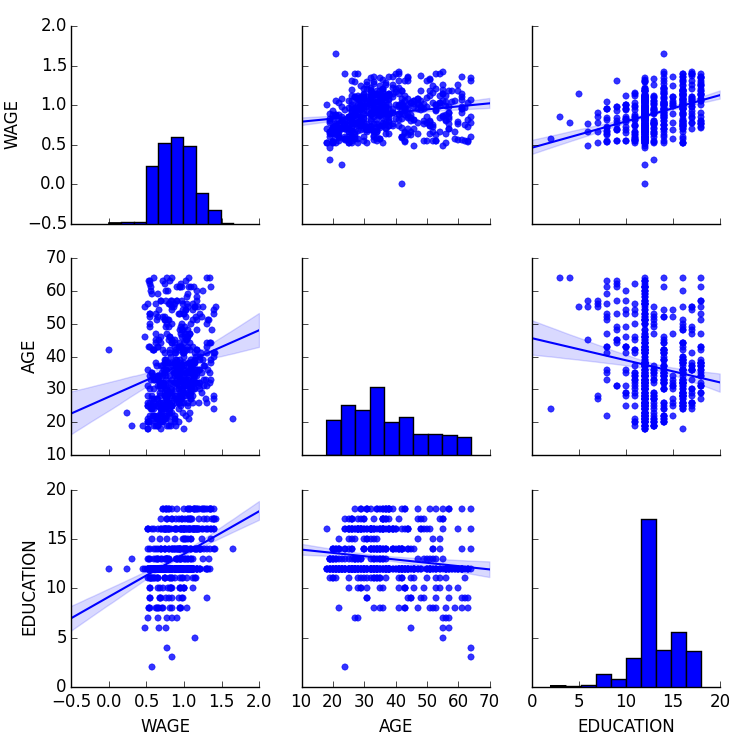
カテゴリ変数を色でプロットすることができます:
>>> seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'],
... kind='reg', hue='SEX')
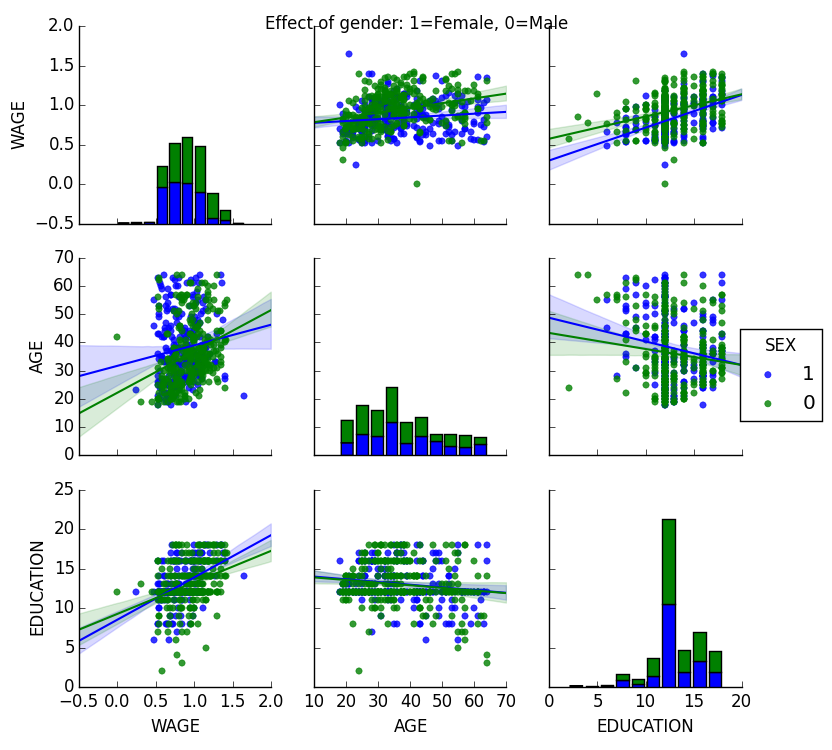
見た目と matplotlib の設定
Seaborn は matplotlib の図のデフォルト設定を変更して、より「現代的」で「Excel 風」な見た目にします。これはインポートのやり方に依存して変わります。デフォルトを以下でリセットできます:
>>> from matplotlib import pyplot as plt
>>> plt.rcdefaults()
ちなみに
seaborn の設定の切り替えや seaborn でのよりよいスタイリングを理解するためには seaborn documentation の関連する節 を参照して下さい。
3.1.4.2. lmplot: 単変量回帰をプロット¶
回帰は1つの変数ともう1つの変数の間の関係を捉えます、例えば賃金と教育のように、これは seaborn.lmplot() でプロットできます:
>>> seaborn.lmplot(y='WAGE', x='EDUCATION', data=data)
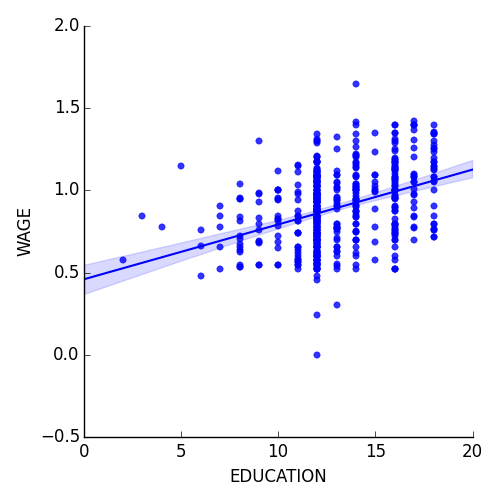
ロバスト回帰
ちなみに
上のプロットでは、いくつかのデータ点が右の主要な点群から外れた点があり、これらは外れ値のようで、主要なデータではなさそうですが、回帰に寄与しているように見えます。
外れ値の影響を受けにくい回帰を計算するには robust model を利用すべきでしょう。それは seaborn で robust=True をプロット関数に渡すか OLS で “Robust Linear Model”, statsmodels.formula.api.rlm() を利用するように置き換えることで実現できます。
3.1.5. 相互関連の検定¶
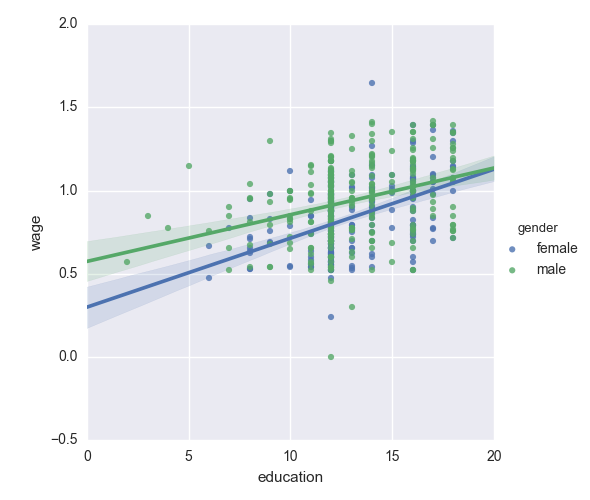
男性の方が女性よりも教育によって賃金が増加しやすいのでしょうか?
ちなみに
上のプロットでは、2つの異なるフィッティングが行なわれています。個体数に対する傾きの分散を検定するための単一のモデルが必要です。これは “interaction” でできます。
>>> result = sm.ols(formula='wage ~ education + gender + education * gender',
... data=data).fit()
>>> print(result.summary())
...
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 0.2998 0.072 4.173 0.000 0.159 0.441
gender[T.male] 0.2750 0.093 2.972 0.003 0.093 0.457
education 0.0415 0.005 7.647 0.000 0.031 0.052
education:gender[T.male] -0.0134 0.007 -1.919 0.056 -0.027 0.000
==========================...
...
女性より男性の方が教育の恩恵を受けやすいと結論づけられますか?
覚えておいて
仮説検定と p値は影響や差に対する 有意さ を表わします
Formulas (とカテゴリ値) はデータの関連の多様な表現を可能にします
可視化 データと単純なモデルがフィットするかわかります!
条件づけ (全体や一部の変動を説明できる要因を追加すること) は解釈を変える重要なモデリングの重要な要素です。
